SPFA算法的全称是:Shortest Path Faster Algorithm,用来求解负权图最短路。实际上,SPFA算法在国际上通称为“队列优化的Bellman-Ford算法”,仅在中国大陆流行“SPFA算法”的称谓。
SPFA的应用场景:
1、能够计算负权图最短路问题;
2、能够判断是否有负环(即:每跑一圈,路径会减小,所以会一直循环跑下去)。
SPFA在形式上和广度(宽度)优先搜索非常类似,不同的是bfs中一个点出了队列就不可能重新进入队列,但是SPFA中一个点可能在出队列之后再次被放入队列,也就是一个点改进过其它的点之后,过了一段时间可能本身被改进(重新入队),于是再次用来改进其它的点,这样反复迭代下去。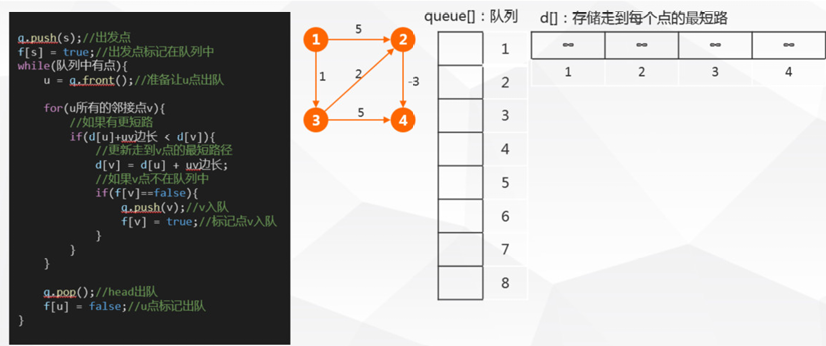
🔍 SPFA 算法核心要点一览
| 知识模块 | 关键知识点 | 说明与要点 |
|---|---|---|
| 算法定位 | Bellman-Ford 的队列优化 | SPFA 是 Bellman-Ford 算法的优化版本,核心思想是通过队列减少不必要的松弛操作。 |
| 核心思想 | 动态逼近 & 惰性松弛 | 使用队列维护待优化的顶点。只有当顶点的最短距离估计值被更新(松弛)后,才将其加入队列,以优化其邻居。 |
| 关键操作 | 松弛操作 | 对于边 (u, v),若 dist[u] + w(u, v) < dist[v],则更新 dist[v]。这是所有最短路径算法的核心。 |
| 数据结构 | 队列 (Queue) & 标记数组 | 队列:用于存储待松弛的顶点(FIFO)。标记数组 (inQueue[]):标记顶点是否已在队列中,避免重复入队。 |
| 距离数组 & 前驱数组 | 距离数组 (dist[]):记录从源点到各点的当前最短距离。前驱数组 (predecessor[]):用于还原最短路径。 | |
| 特有优势 | 处理负权边 | 能处理带有负权边的图,而 Dijkstra 算法在此情况下会失效。 |
| 检测负权环 | 通过判断顶点的入队次数是否超过 ` | |
| 时间复杂度 | 平均情况 (随机稀疏图) | 效率很高,实践中的平均时间复杂度接近 O(E)。 |
| 最坏情况 | 会退化为与 Bellman-Ford 算法相同的 O(V*E),例如在精心构造的稠密图或存在负权环的图中。 | |
| 适用场景 | 含负权边的图 | 当图中存在负权边时,是重要的备选算法。 |
| 需要检测负权环 | 当需要判断图中是否存在负权环时。 | |
| 随机稀疏图 | 在随机的稀疏图上通常表现优异。 | |
| 代码实现 | 初始化 | 设置 dist 数组(源点为0,其余为无穷大),队列初始加入源点,并标记 inQueue[source] = true。 |
| 主循环 | 1. 出队:取出队首顶点 u,并标记 inQueue[u] = false。2. 松弛:遍历 u 的邻居 v,尝试松弛。若成功且 v 不在队列中,则 v 入队并标记。 | |
| 负环检测 | 维护计数数组 count[],顶点 v 每次入队则 count[v]++。若存在某个 `count[v] >= | |
| 优化技巧 | SLF (Small Label First) | 使用双端队列 (Deque)。新顶点入队时,若其 dist 值小于队首,则插入队首;否则插入队尾。可能提升平均性能。 |
| LLL (Large Label Last) | 当队首元素的 dist 值大于当前队列中所有 dist 的平均值时,将其移至队尾。可能避免“卡”在局部劣质路径。 | |
| 常见陷阱 | 忽略负环导致死循环 | 若图中存在负权环,且未实现负环检测,算法可能无法终止(在负环上无限循环松弛)。 |
| 初始化错误 | 务必正确初始化 dist 数组和标记数组。 |
💡 算法原理与实现细节
理解SPFA的关键在于认识它是如何优化Bellman-Ford算法的。Bellman-Ford算法会对所有边进行 V-1 轮松弛,其中很多是无效操作。SPFA的优化在于它并非盲目地进行所有轮次的全局松弛,而是采用了一种“反应式”的策略:只有当某个顶点 u 的最短距离被更新后,才认为由 u 出发的边有可能去优化其邻居顶点 v 的距离。这时才会将 u 放入队列,等待后续处理。这个过程更符合直觉,类似于波纹的扩散。
在实现时,除了基本的队列操作和松弛逻辑,负权环的检测是SPFA的一个重要功能。其原理是:在一个没有负权环的图中,任意两点间的最短路径最多包含 V-1 条边。因此,任何一个顶点最多被松弛(即入队)V-1 次。如果发现某个顶点的入队次数达到了 V 次,那么就可以判定图中存在从源点可达的负权环。
⚖️ 对比与选型:何时选择SPFA?
了解一个算法的优缺点和适用场景,与理解其原理同等重要。为了帮助你更直观地理解SPFA在算法家族中的位置,以及如何在具体问题中做出选择,可以参考下面的决策流程图:
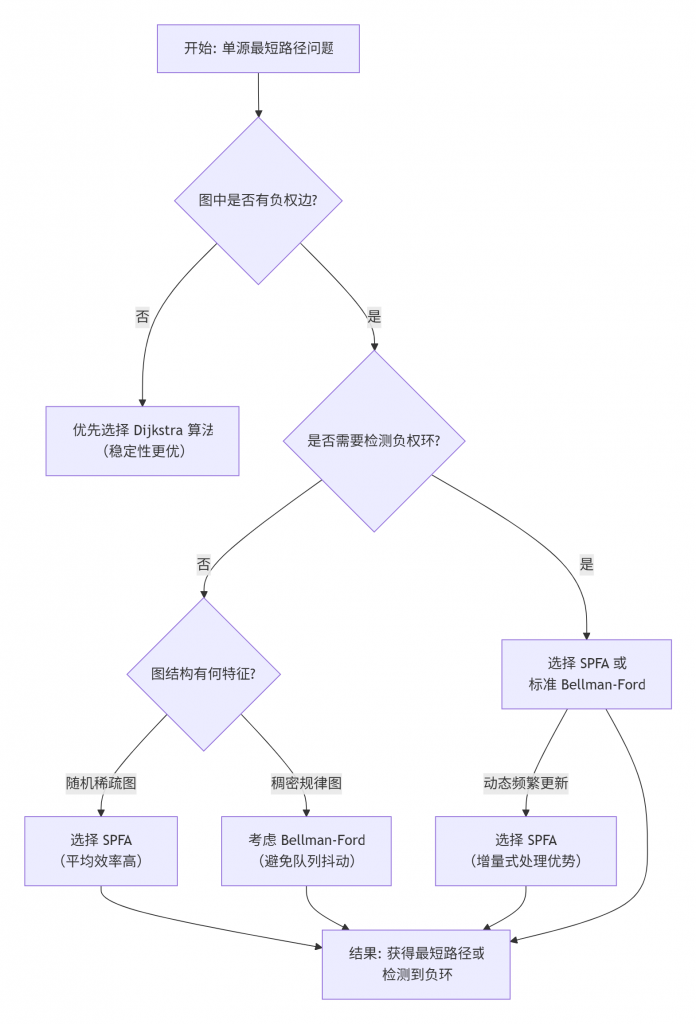
从上图可以看出,SPFA并非一个“万能”算法,它的用武之地非常明确。当你的问题场景满足以下一个或多个条件时,应优先考虑SPFA:
- 存在负权边:这是SPFA的核心应用场景。
- 需要检测负权环:SPFA可以方便地集成负环检测功能。
- 图为随机稀疏图:在这种图上,SPFA的平均表现往往非常出色,接近线性复杂度O(E)。
- 图结构动态变化:如果图需要频繁更新(如增删边),SPFA的增量式处理方式可能更有优势。
反之,如果图中全是非负权边,那么Dijkstra算法(特别是堆优化版本)通常是更稳定、更高效的选择,因为它能保证稳定的O((E+V)log V)时间复杂度,不会出现SPFA的最坏情况。
