选择题（每题2分，共15题）
1、人脸识别应用了哪项技术？
A.生物特征识别
B.超声波
C.蓝牙
D.区块链
2、现有5张分辨率为 720×500 像素的32位真彩色图像。请问要存储这些图像，至少需要多大的存储空间？（至少：如果有多个选项满足要求，选存储空间最小的即可）（ ）。
A.128MB
B.32MB
C.8MB
D.2MB
3、38 | (1 << 6) 的二进制末8位是（ ）。
A.10011011
B.00011011
C.01100110
D.11100100
4、计算机网络中“带宽”这一术语表示( ).
A.计算机位数
B.CPU主频
C.数据传输的速度
D.数据传输的宽度
5、以下关于二叉树的说法中，错误的是( )。
A.叶子节点可能出现在任何一层
B.如果根节点在第1层，第n层最多有2n-1个节点
C.如果根节点在第1层，n个节点组成的完全二叉树深度为log2n + 1
D.如果二叉树非空，有两个孩子的节点可能和叶子节点一样多
6、有一杯水，第一次被小明喝掉了全部的一半少10ml，第二次又被小明喝掉了余下的一半多10ml，这时杯子里还有20ml水，请问这杯水一开始有多少ml？
A.100
B.200
C.150
D.120
7、对数组 {4, 2, 8, 3, 5, 7, 1, 6} 进行升序冒泡排序，会发生( )次交换操作。
A.13
B.14
C.15
D.16
8、中序遍历序列与后序遍历序列相同的二叉树为( )。
A.根结点无左子树
B.根结点无右子树
C.只有根结点的二叉树或非叶子结点只有左子树的二叉树
D.只有根结点的二叉树或非叶子结点只有右子树的二叉树
9、给定有向图的邻接矩阵如下（矩阵从第0行第0列开始），顶点2的入度和出度分别是( )。
A.2,1
B.1,2
C.3,2
D.2,3
10、从10件不同编号的产品（其中次品3件）中，有顺序不放回的任意取出4件，求4件中恰有1件次品的取法数？( )
A.2520
B.105
C.5040
D.210
11、如果A∪B={a1,a2,a3,a4}, 则有序集合对（A, B）有__种可能。
A.81
B.64
C.16
D.17
12、在一个无向图中，如果任意两点之间都存在路径相连，则称其为连通图。下图是一个有6个顶点、9条边的连通图。若要使它不再是连通图，至少要删去其中的（ ）条边。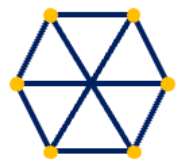
A.6
B.5
C.4
D.3
13、假设某算法的计算时间可用递推关系式 T(n)=T(n-1)+n 表示，T(1)=1，则该算法的时间复杂度为( )
A.O(n)
B.O(nlogn)
C.O(n2)
D.O(2n)
14、将(2, 5, 15, 20)分别存储到某个地址区间为 0~12 的哈希表中，如果哈希函数h(x)=（ ），将不会产生冲突，其中 a mod b 表示 a 除以 b 的余数。
A.x mod 13
B.3x mod 13
C.x2 mod 13
D.Гx/2ꓶ mod 13， 其中Гx/2ꓶ 表示x/2上取整
15、下列前缀表达式中与中缀表达式 e-(a-b)(c+d) 相等的为（ ）。
A.eab-cd+-
B.-e+cd-ab
C.-+dc-bae
D.ba-dc+*e-
阅读程序一（12分）
判断题（正确的选T，错误的选F，每题1.5分）
(1)如果height数组中的输入有负数，则程序会出错。()
(2)程序输出的 ans 小于或等于n。 ()
(3)将12行num[j]>=num[i]”改为“num[j]>num[i]”，程序的输出结果不会改变。()
(4)将18行“num[i]>ans”改为“num[i]>=ans”，程序的输出结果不会改变。()
选择题，每题3分
(5)若输入的数据为
10
1 1 1 1 1 1 1 1 1 1
则程序的输出结果是()。
A.4
B.3
C.2
D.1
(6)若输人的数据为
10
3 2 5 11 12 7 4 10 15 6
因程序的输出结果是( )。
A.4
B.5
C.6
D.7
阅读程序二（15分）
判断题（正确的选T，错误的选F，每题1.5分）
(1)第19行的输入中，如果满足m=n*(n-1)/2,则20~22行的初始化可以省略。()
(2)将第31行的代码换成“for(i=n;i>=1;i–)”，程序结果不受任何影响。( )
选择题（每题3分）
(3)若输入的数据为
4 2
1 2 1
3 4 1
则程序的输出结果是( )。
A. 8
B. 4
C. 2
D. 1
(4)若输入的数据为
4 6
1 2 1
2 3 1
3 4 1
4 1 1
1 3 1
2 4 1
则程序的输出结果是( )。
A.1
B.3
C.5
D.7
(5)若输人的数据为
4 3
1 2 10
2 3 20
3 1 30
则程序的输出结果是( )。
A.30
B.50
C.60
D. 120
(6)若输入的数据为
4 6
1 2 10
2 3 20
3 4 30
4 1 40
1 3 50
2 4 60
则程序的输出结果是()。
A.60
B.100
C.150
D.200
阅读程序三（13分）
判断题（正确的选T，错误的选F，每题1.5分）
1.(1分)若将第12行（ for (int j = 0; j < idx && primes[j] <= N / i; j++) ）中 && primes[j] <= N / i 去掉，则数组st[]一定会越界。 （ ）
2.函数goldSieve运行后，gb[4]的值为true。 （ ）
3.交换30行和31行，程序运行结果不会产生变化。 （ ）
选择题（每题3分）
4.如果输入是：
3
12
244
3001
输出是：
A.
okk
okk
something wrong
B.
okk
okk
okk
C.
something wrong
something wrong
something wrong
D.
something wrong
something wrong
okk
5.将第22行的int i = 1 改为 int i = 0，如果输入是:
3
12
244
3001
输出是：
A.
okk
okk
something wrong
B.
okk
okk
okk
C.
something wrong
something wrong
something wrong
D.
something wrong
something wrong
okk
6.第24行执行的次数最接近以下哪个选项：
A. 1024000
B. 2048000
C. 128000
D. 32000
完善程序一
(高精度计算)由于计算机运算的数据范围表示有一定限制，如整型int表达范围是(-231~231-1)，unsigned long(无符号整数)是(0~232-1)，都约为几十亿，因此在计算位数超过十几位的数时，不能采用现有类型，只能自己编程计算。
高精度计算通用方法：高精度计算时一般用一个数组存储一个数，数组的一个元素对应于数的一位，将数由低位到高位依次存储在数组下标对应的由低到高的位置上。另外，申请数组大小时，一般考虑了最大的情况，在很多情况下表示有富裕，即高位有很多0，可能造成无效的运算和判断，因此一般利用一个整型数据存储该数的位数。下面的程序是一个高精度整数的加法运算，请补充完整程序。
(1)①处应填()。
A.a.num[i]=c[i]-‘0’
B.a.num[a.len-i]=c[i]-‘0’
C.a.num[a.len-i]=c[i]
D.a.num[i]=c[i]
(2)②处应填( )。
A.b.num[i]=d[i]
B.b.num[b.len-i]=d[i]
C.b.num[b.len-i]=d[i]-‘0’
D.b.num[i]=d[i]-‘0’
(3)③处应填( )。
A.(a.num[i]+b.num[i])
B.(a.num[i]+b.num[i])%10
C.(a.num[i]%10+b.num[i]%10)
D.(a.num[i]+b.num[i]-10)
(4)④处应填( )。
A.w.num[i]/10
B.w.num[i]
C.w.num[i]%10
D.w.num[i]-10
(5)⑤处应填( )。
A.w.num[w.len+1]>=0
B.w.num[w.len+1]==0
C.w.num[w.len+1]!=0
D.w.num[w.len +1]>1
完善程序二
(马走日)回溯算法实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试其他路径。回溯法是一种选优搜索法按选向前索以达到目标。但当搜索到某一步时，若发现原先选择并优或达不到目标,则退回一步重新选择，这种走不通就退回去再走的技术称为回溯法，而满足回溯条件的某个状态的点称为回溯点。
马在中国象棋中以日字形规则移动。请编写一段程序，给定rxc大小的棋盘以及马的初始位置(m,n)，要求不能重复盘上的同一个点,计算马有多少途径可以遍历盘上的所有点。
(1)①处应填()。
A. x>=0 || y>=0 || x<r || y<c
B. x>=0 || y>=0 && x<r || y<e
C. x>=0 && y>=0 && x<r && y<c
D. x>=0&&y>=0|| x<r &&y<c
(2)②处应填( )。
A. check(wayr[i]，wayc[i])
B. check(x+wayr[i]，y+wayc[i])
C. !check(x+wayr[i],y+wayc[i])
D. !check(wayr[i],wayc[i])
(3)③处应填( )。
A. mark[wayr[i]][wayc[i]]
B. mark[x+wayr[i]][y+wayc[i]]
C. !mark[wayr[i]][wayc[i]]
D. !mark[x+wayr[i]][y+wayc[i]]
(4)④处应填( )。
A. tot==r*c-1
B. tot==r*c
C. cnt==r*c-1
D. cnt==r*c
(5)⑤处应填()。
A. wayr[i], wayc[i]
B. x-wayr[i], y-wayc[i]
C. x-wayr[i], y+wayc[i]
D. x+wayr[i], y+wayc[i]