迪杰斯特拉算法（Dijkstra）是由荷兰计算机科学家狄克斯特拉于1959年提出的，因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法，解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始，采用贪心算法的策略，每次遍历到起始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止。
Dijkstra算法是典型的单源最短路径算法，主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。
问题描述：在无向图G=（V, E）中，假设每条边e[i]的长度为w[i],找到由顶点V0到其余各点的最短路径。（单源最短路径）
注意：Dijkstra算法适用于边权为正的无向和有向图，不适用于有负边权的图。
算法思想：
设G=（V,E）是一个带权有向图，把图中顶点集合V分成两组，第一组为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径，就将加入到集合S中，直到全部顶点都加入到S中，算法就结束了），第一组为其余未确定最短路径的顶点集合（用U表示），按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外，每个顶点对应一个距离，S中的顶点的距离就是从v到此顶点的最短路径长度，U中的顶点的距离，是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。
算法步骤：
a. 初始时，S只包含源点，即S= {v}, v的距离为0。U包含除v外的其他顶点，即:U={其余顶点}，若V与U中顶点U有边，则正常有权值，若U不是V的出边邻接点，则 权值为 ∞。
b. 从U中选取一个距离V最小的顶点k，把k，加入S中（该选定的距离就是V到k的最短路径长度）。
c. 以k为新考虑的中间点，修改U中各顶点的距离；若从源点v到顶点u的距离（经过顶点k）比原来距离（不经过顶点k）短，则修改顶点u的距离值，修改后的距离值的顶点 k的距离加上边上的权。
d. 重复步骤b和c直到所有顶点都包含在S中。
重点需要理解这句拗口的“按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径度”。
最短路径举例，如下图，计算点1到5的最短距离：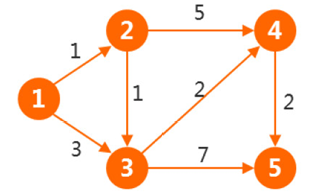
dis[]:记录从出发点走到每个点的最短路：
vis[]:记录哪些点的最短路的值已经确定：
如何确定一个点t,从出发点s到该点t的路径长度就是最短的？ 在没有确定的点的集合中，找一个最小值！
注意：不能用INT_MAX来表示从s走不到该点，因为INT_MAX+任意的数会溢出。 而：0x3f3f3f3f,表示无穷大是很好的选择，因为这个数就算加上自己，也不会超过 int。
如在初始化数组a时,可以使用memset(a,0x3f,sizeof(a)),因为0x3f3f3f3f的每个字节都是0x3f。
迪杰斯特拉算法（Dijkstra）的时间复杂度O(n2)。
优先队列BFS-Dijkstra堆优化：在没有负权值图的最短路的问题中，我们每次取出当前代价最小的状态进行扩展，由于该状态已经是最优的了，队列中的其他状态的当前代价都不小于该值，因此以后就不可能再次更新该值。
为了维护当前的最小代价，我们将扩展出来的所有点存到优先队列(priority_queue) 中，这种求解最短路的方法，就是优先队列BFS，其实也就是改进版的dijkstra算法。
该算法的时间复杂度为：O(n*log(n)), 其中的log(n)是用于维护优先队列(二叉堆) 的时间复杂度。
在该算法中，当每个状态第一次从队列中被取出时，就得到了从起始状态到该状态的最小代价。
🔍 Dijkstra 算法核心知识要点
在算法学习中，掌握 Dijkstra 算法是关键一步，它解决了带权图的单源最短路径问题。
| 知识模块 | 关键知识点 | 说明与要点 |
|---|---|---|
| 核心思想 | 贪心策略 (Greedy) | 从源点出发，每一步都选择当前已知最短路径的顶点，并以此更新其邻居的距离，直到所有顶点的最短路径均被确定。 |
| 基本概念 | 松弛操作 (Relaxation) | 对于边 (u, v)，如果 dist[u] + w(u, v) < dist[v]，则用该值更新 dist[v]。这是最短路径算法的核心操作。 |
| 数据结构 | 图的存储 | 常用邻接矩阵或邻接表来存储图结构。 |
距离数组 (dist[]) | 记录从源点到每个顶点的当前最短距离估计，初始时源点为0，其余为无穷大 (∞)。 | |
集合 S / 标记数组 (visited[]) | 用于记录已确定最短路径的顶点集合。 | |
| 关键优化 | 优先队列 (堆) | 使用堆（如最小堆）来高效选取当前距离最小的顶点，将算法复杂度从 O(V²) 优化至 O((V+E) log V)。 |
| 前提条件 | 非负权边 | 图中所有边的权重必须非负。存在负权边时，Dijkstra 算法可能得出错误结果。 |
| 时间复杂度 | 朴素实现 | O(V²)，适合稠密图。 |
| 堆优化实现 | O((V+E) log V)，适合稀疏图（边数 E 远小于 V² 时）。 | |
| 典型应用 | 单源最短路径 | 求从一个固定源点到图中所有其他顶点的最短路径，产生一棵最短路径树。 |
| 路由算法 | 在网络路由中用于寻找最优路径。 | |
| 实际建模 | 如地图导航中寻找最短行车路线。 | |
| 代码实现 | 初始化 | 设置 dist 数组和标记数组的初始状态。 |
| 主循环 | 1. 选取未处理顶点中 dist 最小的顶点 u。2. 标记 u 为已处理。 3. 松弛 u 的所有未处理邻居 v。 | |
| 路径重建 | 可维护一个 predecessor 数组，在松弛操作时记录前驱节点，最终逆向回溯得到完整路径。 | |
| 常见陷阱 | 负权边 | 算法无法处理包含负权边的图，因为其贪心选择性质会遭到破坏。 |
| 初始化与溢出 | 距离初始化应为“无穷大”，但后续计算需注意防止 ∞ + 权值 导致的算术溢出。 |
💡 从理解到应用：学习路径建议
- 循序渐进理解思想
Dijkstra 算法的正确性基于一个关键前提：当所有边权非负时，当前未确定顶点中距离最小的那个，其距离就是最终的最短距离。你可以这样理解：每次从集合 S 外选择一个离源点最近的点 u 加入 S，并更新所有与 u 相邻的点的距离，直到所有点都加入 S。理解这一点是理解整个算法的基础。 - 动手实现两种版本
- 朴素实现 (O(V²))：使用数组存储，每次线性扫描寻找最小
dist的顶点。这有助于你理解算法的核心步骤。 - 堆优化实现 (O((V+E) log V))：使用优先队列（最小堆）来高效获取最小
dist顶点。这是实际应用中的主流实现方式。建议你先完成朴素实现，再加入堆优化，体会优化带来的效率提升。
- 朴素实现 (O(V²))：使用数组存储，每次线性扫描寻找最小
⚠️ 注意常见误区
- 负权边的限制：这是 Dijkstra 算法最重要的使用前提。如果图中存在负权边，贪心选择将不再正确，需要使用能够处理负权边的 Bellman-Ford 等算法。
- 环路的处理：Dijkstra 算法要求图没有负权环。在非负权图中，即使存在环路，由于边权非负，算法也能正确工作，因为绕行环路不会让路径长度减小。
- “已确定”的含义：一个顶点一旦被标记为“已确定”（加入集合 S），其
dist值就不再会被更新。这是算法高效的关键，但也决定了它不能处理负权边。
💎 总结与进阶
Dijkstra 算法是图论中非常基础和重要的算法。它的核心在于贪心策略和松弛操作。掌握它的关键点包括：理解其贪心选择性质、熟悉松弛操作、掌握两种实现方式（特别是堆优化）、牢记非负权边的使用前提。