Bellman-Ford 算法 给定一张有向图,若对于图中的某一条边(x,y,z),有 dist[y]≤dist[x]+z成立,则称该边满足三角形不等式。若所有边都满足三角形不等式,则 dist 数组就是所求最短路。
Bellman-Ford 算法的执行过程 很简单,就是对边集合进行 N – 1 轮迭代松弛,每一轮执行m次(边集合的大小为 m)操作。具体流程如下:
1.扫描所有边(x,y,z),若 dist[y]>dist[x]+z ,则用 dist[x]+z 更新 dist[y]。
2.重复上述步骤,直到没有更新操作发生。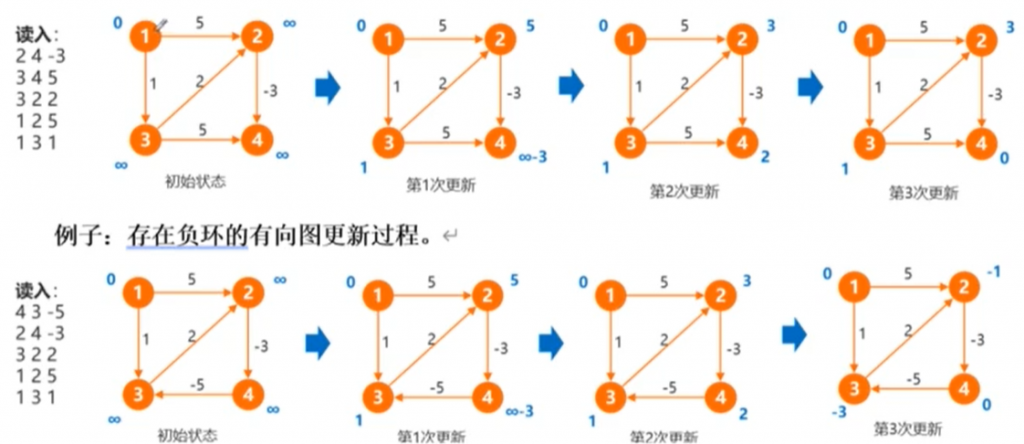 经过k次循环,求出的dist数组代表了:从1号点出发,在经过不超过k条边的情况下,到每个点的最短路。
经过k次循环,求出的dist数组代表了:从1号点出发,在经过不超过k条边的情况下,到每个点的最短路。
性能分析 Bellman-Ford 算法中共存在 n 次对边集合的迭代松弛,边集合的大小为 m ,所以Bellman-Ford 算法的时间复杂度为 O(n*m)。
🔍 核心知识要点速览
Bellman-Ford 算法是图论中求解单源最短路径问题的一个重要算法,特别是它能处理 Dijkstra 算法束手无策的负权边情况。
| 知识模块 | 关键知识点 | 说明与要点 |
|---|---|---|
| 核心思想 | 动态规划与松弛操作 | 通过 ** |
| 关键操作 | 松弛操作 (Relaxation) | 对于边 (u, v, w),若 dist[u] + w < dist[v],则更新 dist[v]。这是算法的基石。 |
| 独特优势 | 处理负权边 | 能处理图中带有负权重的边,而Dijkstra算法在此情况下会失效。 |
| 检测负权环 | 算法完成后,若再进行一次松弛操作仍有边可被松弛,则说明图中存在从源点可达的负权环。 | |
| 算法步骤 | 1. 初始化 2. 迭代松弛 3. 负环检测 | 1. 初始化源点距离为0,其余点为无穷大。 2. 进行 ** |
| 时间复杂度 | O( | V |
| 常见应用 | 1. 含负权边的图的最短路径 2. 负权环检测 3. 限制路径边数的最短路径 4. 差分约束系统 | 尤其适用于金融套利检测、网络路由等需要处理负权或检测负环的场景。 |
| 实现技巧 | 备份数组防止“串联” | 在同一次迭代中,应使用上一轮迭代后的距离值进行松弛,避免本次迭代已更新的值被误用。 |
| 与Dijkstra对比 | 贪心 vs. 动态规划 | Dijkstra 基于贪心,不能有负权边;Bellman-Ford 基于动态规划,可处理负权边,但较慢。 |
💡 算法原理与实现细节
理解Bellman-Ford算法的关键在于认识其松弛操作和动态规划的本质。算法通过 **|V|-1 轮松弛来保证找到最短路径,是因为在不存在负权环的图中,任意两点间的最短路径最多包含 |V|-1 条边**。
负权环的检测原理是算法的一个亮点。如果经过 |V|-1 轮松弛后,还能继续松弛,说明存在一条边数大于等于 |V| 的路径还能被优化。根据鸽巢原理,该路径中必有节点被重复访问,即存在环,且此环的权重和为负才能使路径无限缩短。
在实现时,需要注意“串联”现象。即在同一次迭代中,如果直接使用当前轮次更新后的距离值去松弛后续的边,可能会导致本该在第k轮才能确定的最短路径,在第k次迭代中就“提前”传播出去了。因此,需要在每次迭代开始时,备份上一轮的距离数组,并使用备份数组来进行本轮所有的松弛操作。
⚖️ 对比与选型:何时选择Bellman-Ford?
了解一个算法的优缺点和适用场景,与理解其原理同等重要。为了帮助你更直观地理解Bellman-Ford在算法家族中的位置,以及如何在具体问题中做出选择,可以参考下面的决策流程图:
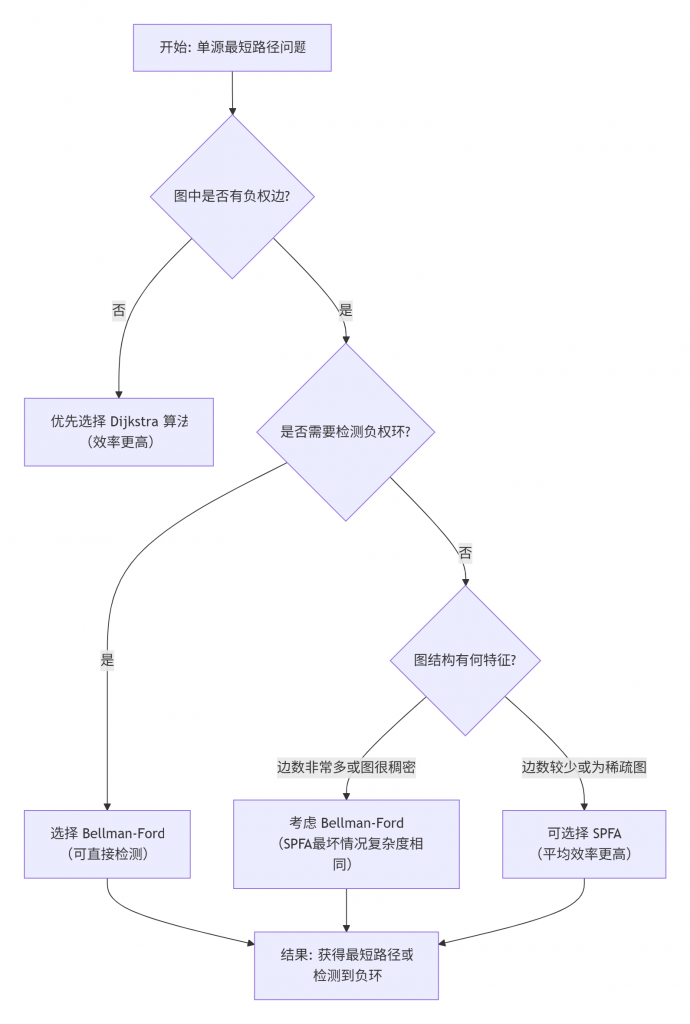
从上图可以看出,Bellman-Ford算法在特定场景下具有不可替代的价值。当你的问题满足以下一个或多个条件时,应优先考虑Bellman-Ford算法:
- 存在负权边:这是Bellman-Ford的核心应用场景。
- 需要检测负权环:Bellman-Ford可以直接检测图中是否存在从源点可达的负权环。
- 限制路径边数:例如求解“经过不超过k条边的最短路径”问题,Bellman-Ford的迭代次数特性天然适合。
- 图结构非常稠密或对最坏情况效率有要求:虽然SPFA是Bellman-Ford的优化,平均效率高,但其最坏时间复杂度与Bellman-Ford相同。在恶劣情况下,Bellman-Ford稳定的O(|V|·|E|)可能更可预测。
反之,如果图中全是非负权边,那么Dijkstra算法(特别是堆优化版本)是更高效的选择。如果图中存在负权边,但你不需要检测负环,且图比较稀疏,那么SPFA算法(Shortest Path Faster Algorithm,Bellman-Ford的队列优化版本)的平均表现通常会更好。
