记忆化搜索 是一种通过记录已经遍历过的状态的信息,从而避免对同一状态重复遍历的搜索实现方式。因为记忆化搜索确保了每个状态只访问一次,它也是一种常见的动态规划实现方式。
记忆化搜索的实现方法:
1、写出这道题的暴搜程序(最好是 dfs)。
2、将这个 dfs 改成「无需外部变量」的 dfs。
3、添加记忆化数组。
举个例子,比如「斐波那契数列」的定义是:f(0) = 0, f(1) = 1, f(n) = f(n – 1) + f(n – 2)。如果我们使用递归算法求解第 n 个斐波那契数,则对应的递推过程如下:
如果我们使用递归算法求解第 n 个斐波那契数,则对应的递推过程如下: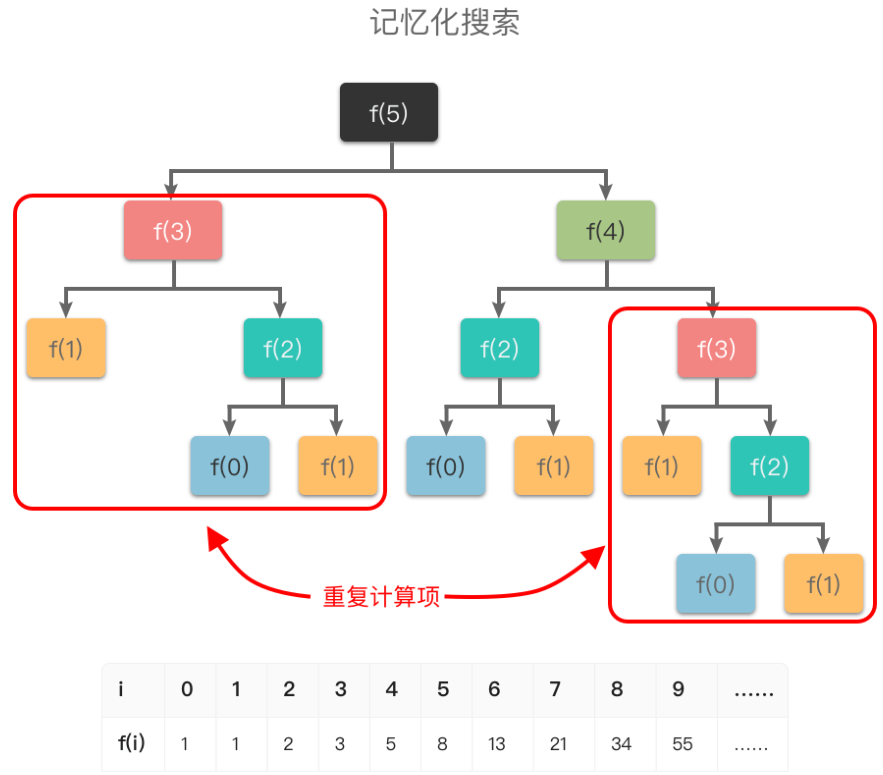
为了避免重复计算,在递归的同时,我们可以使用一个缓存(数组或哈希表)来保存已经求解过的 f(k) 的结果。如上图所示,当递归调用用到 f(k) 时,先查看一下之前是否已经计算过结果,如果已经计算过,则直接从缓存中取值返回,而不用再递推下去,这样就避免了重复计算问题。
记忆化搜索与递推区别
「记忆化搜索」与「递推」都是动态规划的实现方式,但是两者之间有一些区别。
记忆化搜索:「自顶向下」的解决问题,采用自然的递归方式编写过程,在过程中会保存每个子问题的解(通常保存在一个数组或哈希表中)来避免重复计算。
优点:代码清晰易懂,可以有效的处理一些复杂的状态转移方程。有些状态转移方程是非常复杂的,使用记忆化搜索可以将复杂的状态转移方程拆分成多个子问题,通过递归调用来解决。
缺点:可能会因为递归深度过大而导致栈溢出问题。
递推:「自底向上」的解决问题,采用循环的方式编写过程,在过程中通过保存每个子问题的解(通常保存在一个数组或哈希表中)来避免重复计算。
优点:避免了深度过大问题,不存在栈溢出问题。计算顺序比较明确,易于实现。
缺点:无法处理一些复杂的状态转移方程。有些状态转移方程非常复杂,如果使用递推方法来计算,就会导致代码实现变得非常困难。
根据记忆化搜索和递推的优缺点,我们可以在不同场景下使用这两种方法。
适合使用「记忆化搜索」的场景:
问题的状态转移方程比较复杂,递推关系不是很明确。
问题适合转换为递归形式,并且递归深度不会太深。
适合使用「递推」的场景:
问题的状态转移方程比较简单,递归关系比较明确。
问题不太适合转换为递归形式,或者递归深度过大容易导致栈溢出。
