A 遍历每一个数字作为被除数,然后试除其他所有的除数,那么两层循环的时间复杂度是 O(n2)。接着,想一想上述的运算过程有哪些计算时多余的,可以省去的。
1、任何一个数字 a[i] 如果出现2次以上,那么这个数字 a[i] 不需要计算,肯定能够被另外一个自己整除。(还有更特殊的是:如果输入数组中有数字1出现,那么其他的数都能找到整除的数:1出现2次以上,最终结果显然为0;1只出现1次,那么最终结果就是1.)
2、我们在计算一个整数数字的因子数量时,做过更小规模的运算:一个数 a[i] 作为被除数,那么除数 j 或商一定是小于等于这个数字的(j==1的情况在此题要注意)。只要将被除数a[i],遍历除数 j 范围1~sqrt(a)之间,得到商。对于数组中的任意一个 a[i] ,如果存在除数j或商存在于数组中,那么说明 a[i] 就能找到被整除的数字(1做除数时,商是自己,那么商要排除)。

B 给一些经过双关键字排序(贡献为第一关键字,名字为第二关键字)的人名,贡献多的资历一定浅,贡献相同的无法确定大小关系。直接找到字典序非递减的地方可以找到大小关系,建图。使用map存储姓名和下标的关系,这样方便在存图时找到对应的下标。

C
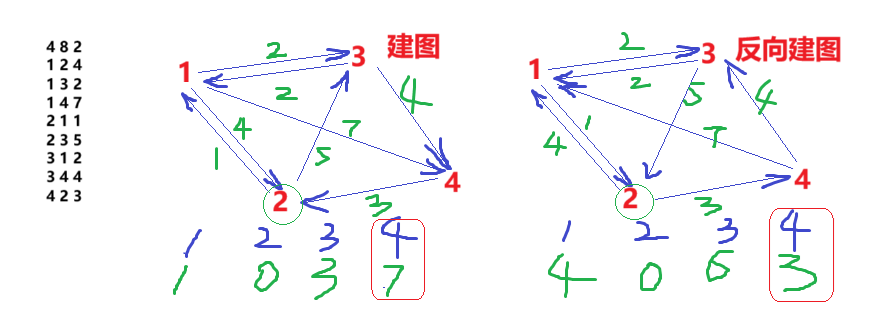
1、计算点x到各个点的最短路;
2、计算各个点到点x的最短路,直接反向建图即可,利用反向建图,把问题也变成了计算点x到各个点的最短路。

D 考虑每加进一个点会对前 i−1 个点的影响。1、产生具有舒适度的奶牛。2、将以前加入的奶牛覆盖(替换掉,也就是同一个位置至多只有一头奶牛)。于是我们就可以发现对于前 i 个奶牛, ans 可由前 i−1 个奶牛状态得到,并且发现如果存在舒适的奶牛,取消他舒适的奶牛是必须要加奶牛的。加入的那个点很显然也是满足上述两种影响.
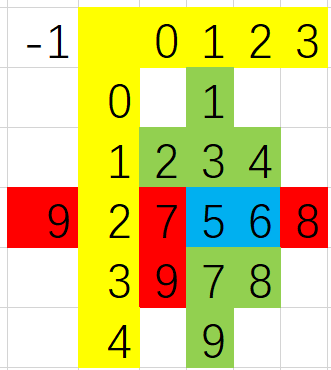
- 存图的时候下标可能会超出边界,就考虑极限,让每个坐标的值加 1000.
- 不要忘记加上的点自身也可能会是舒适的奶牛,所以不要忘记递归该点。

