与KMP类似,AC自动机也是用来处理字符串匹配的问题。与KMP不同的是,KMP用来处理单模式串问题,即问模式串T是否是主串S的子串,而AC自动机则能处理多模式串的问题。
AC自动机处理的常见问题如:给出n个单词Ti,再给出一段文章S,问有多少个单词在文章里出现了。
流程
(1)我们将所有的模式串构建成一棵Trie树。
(2)主串与模式串的匹配
- 假设现在匹配到节点u,即我们得到了一个从根到u点组成的字符串,它代表的是模式串中某个串的前缀T[1…j],也是主串的一段子串S[i-j+1…i]。
- 若S[i+1]和T[j+1]能够匹配,即trie上的u点存在字符为S[i+1]的转移边,那么i加一,u变为走转移边到达的下一个节点。
- 当在u匹配失败即Trie上的u点不存在字符为S[i+1]的转移边时,我们需要找到另一个串,使得它有尽量长的前缀与u所代表的串的后缀相等,即T’[1…k] = T[j-k+1…j],其中T’[1…k]也对应着Trie中的某个节点v。此时我们令u等于v,j等于k,继续判断S[i+1]和T’[j+1]是否能够匹配。
(3)建立nxt数组
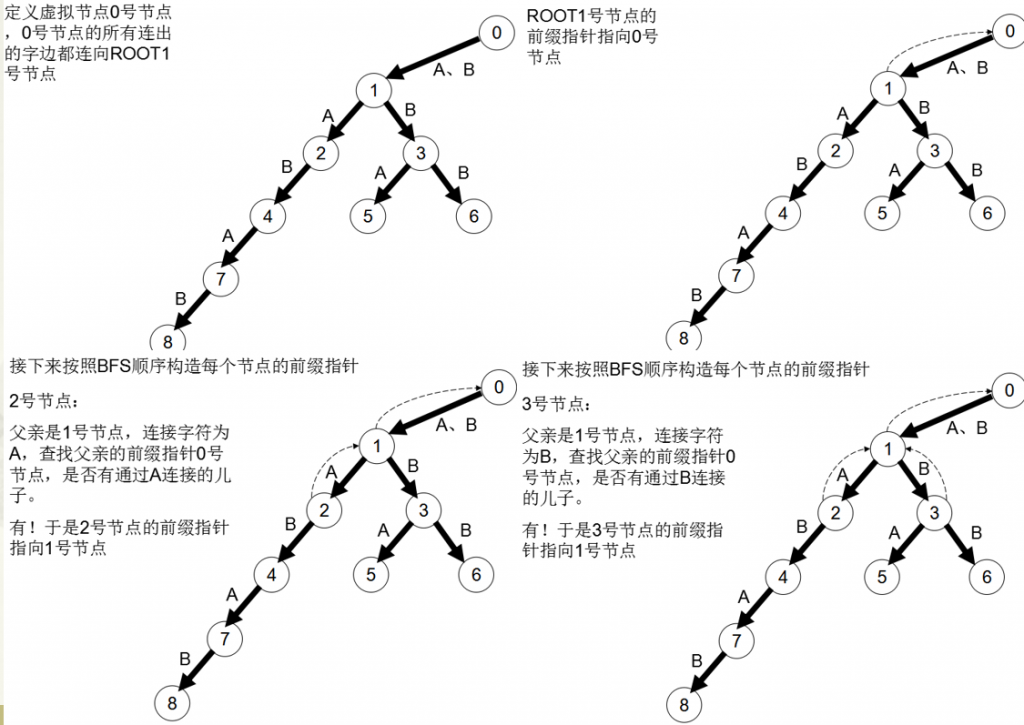
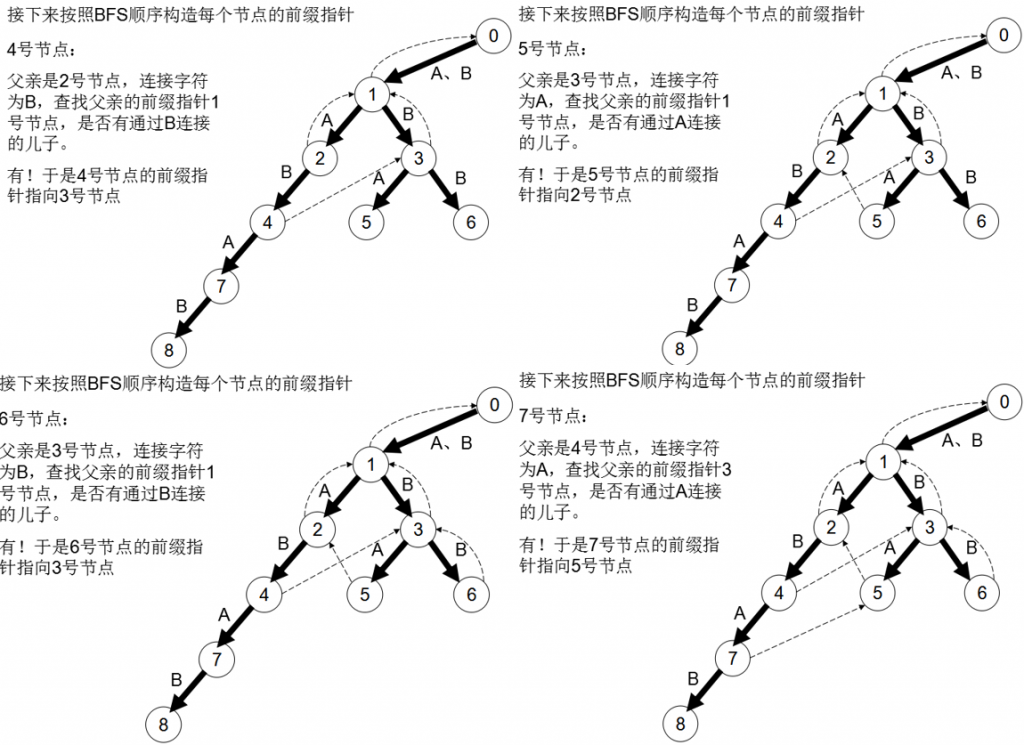
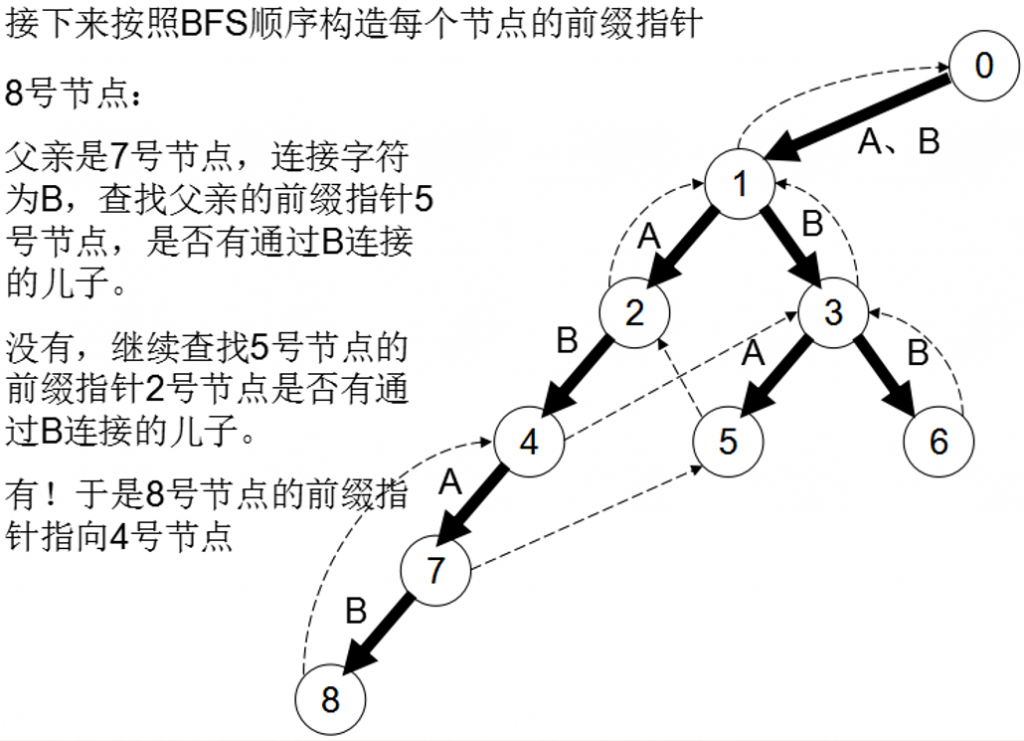
- nxt数组也就是前缀指针,也就是所有满足T'[1…k] = T[j-k+1…j]的k(k < j)的最大值所对应的节点编号。
- nxt[u]的深度是小于节点u的,因此我们可以按节点的深度大小,也就是BFS的顺序来构建nxt数组。
- 与KMP类似,我们设v,u表示字符串T'[1..j], T[1..i],其中v是u的后缀且nxt[u]=v。枚举u的转移边指向的点x,现在我们要求出nxt[x]。若T'[j+1]=T[i+1],也就是下一位仍然匹配,那么设v的相同字符转移边指向的点为y,令nxt[x]等于y。否则T'[j+1]与T[i+1]失配,我们令v=nxt[v],即跳到字符串v的后缀nxt[v]处,按照以上的过程继续判断是否匹配。若跳到空节点,那么无法匹配,nxt[x]=0。
- 下面,我们用实例描述建立nxt数组(即下述的前缀指针)的过程:
实现
构建AC自动机的Trie与普通Trie无异:
1.void make()
2.{
3. int len = strlen(s), u=1;
4. for (int i=0; i<len; ++i)
5. {
6. int c = s[i]-‘A’;
7. //将’A’~’Z’转为0~25的数字
8. if (!ch[u][c]) ch[u][c] = ++tot; //建立新节点
9. u = ch[u][c];
10. }
11. bo[u] = 1; //有以u结尾的字符串,打上标记
12.}
构建nxt数组:
1.void bfs() //通过bfs构建nxt数组
2.{
3. for (int i=0; i<=25; ++i)
4. ch[0][i] = 1; //为了方便将0的所有转移边都设为根节点1
5. que[1] = 1; nxt[1] = 0; //若在根节点失配,则无法匹配字符
6. for (int q1=1,q2=1; q1<=q2; ++q1)
7. {
8. int u = que[q1];
9. for (int i=0; i<=25; ++i)
10. {
11. if (!ch[u][i]) ch[u][i] = ch[nxt[u]][i]; //此处为优化
12. else {
13. que[++q2] = ch[u][i]; // 若有这个儿子则将其加入队列中
14. int v = nxt[u];
15. while (v > 0 && !ch[v][i]) v = nxt[v];
16. nxt[ch[u][i]] = ch[v][i];
17. }
18. }
19. }
20.}
- 为什么当我们发现不存在u的转移边i时,可以令ch[u][i]等于ch[nxt[u]][i]?
- 其实这是为了优化时间。因为在具体问题中,若不存在ch[u][i]的转移边,往往需要沿u的前缀指针走到第一个满足存在字符i的转移边的点v,得到ch[v][i],那么就可直接将ch[u][i]赋值为ch[v][i]即ch[nxt[u]][i]。
- 也正是这个原因,在构建nxt数组时,我们并没有处理v的转移边i不存在的情况,而是直接令nxt[ch[u][i]] = ch[v][i] (其中ch[v][i]也在之前就处理好了)。
匹配:
1.void find()
2.{
3. int u = 1, k;
4. for (int i = 0; i <= m; ++i)
5. {
6. k = ch[u][a[i]];
7. while (k > 1)
8. {
9. ans += bo[k];
10. bo[k] = 0;
11. k = nxt[k];
12. }
13. u = ch[u][a[i]];
14. }
15. return;
16.}
