A star算法最早可追溯到1968年，在IEEE Transactions on Systems Science and Cybernetics中的论文A Formal Basis for the Heuristic Determination of Minimum Cost Paths中首次提出。A*算法是把启发式方法（heuristic approaches）如BFS（完全使用贪心策略），和常规方法如Dijsktra算法结合在一起的算法。有点不同的是，类似BFS的启发式方法经常给出一个近似解而不是保证最佳解。然而，尽管A star基于无法保证最佳解的启发式方法，A star 却能保证找到一条最短路径。
启发式搜索(Heuristically Search)又称为有信息搜索(Informed search)，它是利用问题拥有的启发信息来引导搜索，达到减少搜索范围、降低问题复杂度的目的，这种利用启发信息的搜索过程称为启发式搜索。
启发式策略：可以通过指导搜索向最有希望的方向前进，降低了复杂性。通过删除某些状态及其延伸，启发式算法可以消除组合爆炸，并得到令人能接受的解。
1、A*(A-Star)算法是一种静态路网中求解最短路径最有效的直接搜索方法。
2、A*算法的核心思想：使用优先队列 BFS，并结合估价函数，每次取出优先队列中总代价最低的点进行 BFS 扩展。这种带有估价函数的优先队列 BFS 算法，就是 A* 算法。
例子:求S点到T点的最短路。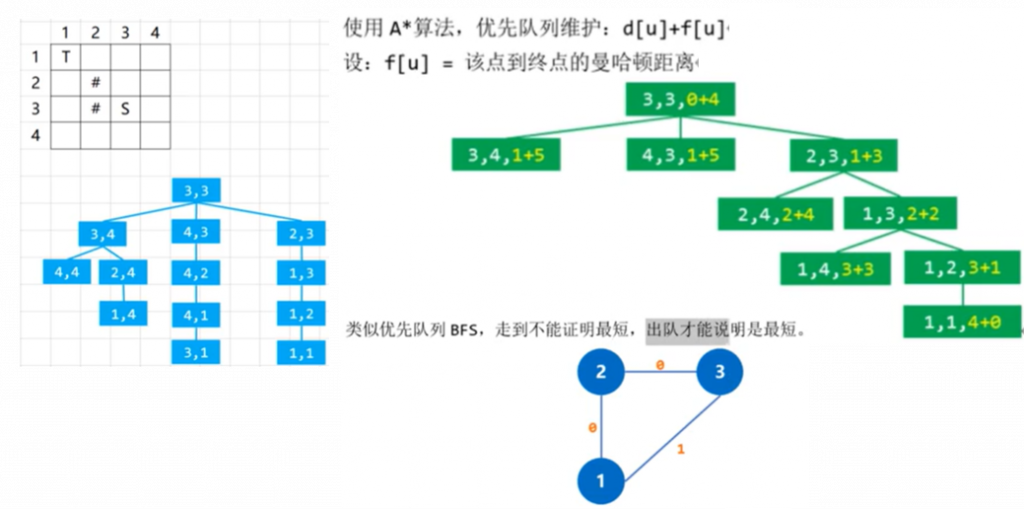
3、A*算法的核心要点:
A.设f(x)代表了x点到终点的估计值，g(x)代表了x点到终点的最终实际值，则定要满足:f(x)≤ g(x)，也就是:估计值必须≤最终实际值，估价函数才有意义。
⚪ 当f(x)=0时，A*算法退化为普通的优先队列BFS的算法;
⚪ 当问题无解时，A*算法会退化为朴素的BFS，但由于A*算法要维护优先队列，因此其效率低于朴素的BFS。
B、目标状态在第1次从优先队列取出时，就得到了最优解。
C、搜索空间比较庞大且问题一定有解时，A*算法的优势才会比较明显。
D、出队就是最小距离的性质，只对终点成立，对其他的点不一定成立，且每个点可能会被讨论多次。
相关说明：
(1) 为什么终点出队说明是最短?
假设 u 点出队，到u点的最短路为 d(u), u 点到终点的估价值为 f(u)，实际值为 g(u)
因为 f(u)≤g(u)
所以 d(u)+f(u)≤d(u)+g(u)
如果u点出队，说明 d(u)+f(u) 是当前队列的最小值，如果该值不是最优解，说明队列中有比其更小的值，与优先队列维护最小值的性质矛盾，因此 u 点出队时，一定能得到 u 点的最优解。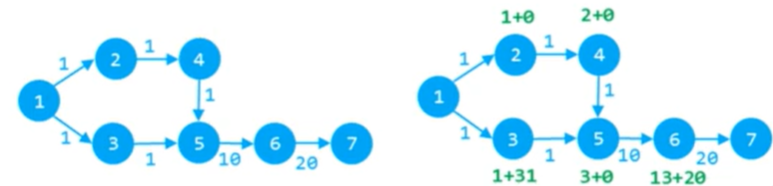
(2) 为什么非终点出队，不一定是最优解？举例:
设：1,2,4,5点的f(x)=0，走其余点 f(x)=g(x)，A*算法对估价函数的要求是f(x)<g(x)因此，设置2种不同的估价函数并不影响算法的正确性。则：d(x)+f(x)的结果将如图所示
讨论发现:
A. 点5出队时，到点5的最短路计算出来是3，这并不是最优解，只是因为 1,2,4,5 点的估价函数较小，因此点5先出队。
B. 当走到点6时， d(x)+f(x)的最小值不是点6，而是点3，用此有机会更正之前错误的解，重新用点 3更新点 5。