选择题（每题2分，共15题）
1、已知十进制中的18在x的进制中的表示为24，即(18)10=(24)x，则这个x进制为()进制。
A.9
B.8
C.7
D.6
2、根据网址的域名 http://www.jiangsu.gov.cn/,可以判断出该网站是()类型的网站。
A.商业机构
B.政府机构
C.军事机构
D.组织结构
3、与计算机硬件关系最密切的软件是()。
A.编译系统
B.操作系统
C.游戏系统
D.数据库系统
4、下列程序段执行后s的值为()。
int i=1, s=0;
while(i++)
if(!(i%3)) break;
else s+=i ;
A.6
B.3
C.2
D.以上都不对
5、将19分解成3个不重复数字(1~9)之和(不计顺序)的方法有()种。
A.6
B.5
C.4
D.3
6、甲、乙、丙三位同学选修课程，在四门课程中，甲选修两门，乙、丙各选修三门，则不同选修方案共有()种。
A.36
B.48
C.64
D.96
7、已知某二叉树的先序遍历序列是 ABDCE，中序遍历序列是 BDAEC，则该二叉树的后序遍历为()。
A.BDECA
B.DBECA
C.DBCEA
D.BDCEA
8、计算机启动时，可以通过存储在( )中的引导程序引导操作系统。
A.ROM
B.RAM
C.Cache
D.CPU
9、表达式a+bc-(d+e)的前缀形式是( )
A.abc+de+-
B.-+abc+de
C.-+abc+de
D.abcde*++-
10、小军在家玩关灯游戏，小军家的灯有三种颜色分别是白、黄、红。按1下白灯亮，按2下灯灭，按3下黄灯亮，按4下灯灭，按5下红灯亮，按6下灯灭，再按又是白灯亮，以此循环。当按到49次和100次时灯的状态是( )。
A.灯灭，灯灭
B.红灯亮，灯灭
C.白灯亮，红灯亮
D.白灯亮，灯灭
11、704与2048的最小公倍数是()。
A.45056
B.22528
C.180224
D.90112
12、在( )的情况下，函数 A V B 运算的结果是逻辑“0”。
A.A和B全部是1
B.A和B任一是1
C.A和B全部是0
D.A和B任一是0
13、小明夫妇请了小刚夫妇和小伟夫妇来他们家玩扑克。这种扑克游戏有一种规则：夫妇两人不能一组。小明和小红一组，小刚的队友是小伟的妻子，琳达的丈夫和小丽一组。那么这三对夫妇分别为( )
A.小明-小丽，小刚-琳达，小伟一小红
B.小明-琳达，小刚-小红，小伟-小丽
C.小明-小丽，小刚-小红，小伟一琳达
D.小明-小红，小刚-小丽，小伟-琳达
14、4人过桥，每人单独过桥分别需要用时1分、2分、5分、10分，过桥需要灯(只有一盏),一次只能2人一起过(意味着需要有人送灯回来)，过桥时间以用时多的人为准，则4人全部过桥时间最少需要()分。
A.15
B.16
C.17
D.18
15、2000 年,华人学者姚期智因在计算理论(包括伪随机数生成、密码学与通信复杂度)方面的突出成就而荣获()
A.图灵奖
B.奥斯卡奖
C.诺贝尔奖
D.普利策奖
阅读程序一（选择题选T或者F，1.5分每题；单选题3分每题）：
函数trans()实现了将十六进制字符串中某一字符转化成十进制数字的作用，例如字符’d’换转化成13。
在主函数中会循环输入n个字符串，字符串中的每一位都会通过trans()函数转化成十进制数，然后再通过左移和位运算会生成4位二进制数，最后将每一位2进制数按照1输出，0输出’ ‘（一个空格）的规则进行输出。 例如输入：
1
ff
先将’f’转化成15，再将15转化成二进制下的1111，再按照规则输出”****”，最终输出为********
判断题：
1）(1分) 若输入的字符串中某一字符为’c’，trans()函数对应返回值为13。（）
T. 正确
F. 错误
2）(1分) 若输入字符串为f0f，则对应的那一行输出仅包含一个空格。（）
T. 正确
F. 错误
3）字符串”70″和字符串”n0″对应的那一行输出是一样的。（）
T. 正确
F. 错误
单选题：
4）若输入字符串为xtl，则输出为（）。
5）.如果想要输出下列的图案，则输入应为（）。
A.
8
ff 02 04 08 10 20 40 ff
B.
8
ff 02 04 08 80 20 40 ff
C.
8
ff 02 04 08 08 02 04 ff
D.
8
ff 20 40 80 08 02 04 ff
6）下列哪项输入字符串对应的那一行输出字符串为回文字符串(即从前往后和从后往前均为同一字符串)( )。
A. c56a3
B. h72c9
C. j8ui7
D. a76d5
阅读程序二：（选择题选T或者F，1.5分每题；单选题3分每题）：
数据范围： 1≤n≤25 , 0≤k≤109
请阅读程序，完成下面的判断题和单选题。
(提示： 230=1073741824，231=2147483648
判断题：
1）(1分) k必须<=30，否则程序会报错。
A. 正确
B. 错误
2）(1分) 第 16 行，当need=0，k=0时，若把的<= 改成 < ，程序输出不变。
A. 正确
B. 错误
3）第14行，若改成从for(int i = 0; i <= 30; ++i) ，程序输出不变
A. 正确
B. 错误
单选题 :
4）输入以下数据后: 3 2 2 1 1 。输出的数据为（）
A. 1
B. 2
C.1073741824
D.2147483647
5）输入以下数据后：4 4 3 1 3 1。输出的数据为（）
A. 1073741824
B. 1073741825
C. 2147483646
D. 2147483647
6）输入以下数据后：1 30 0。输出的数据为（）
A. 0
B. 1
C. 2147483646
D. 2147483647
阅读程序三：
输入数据范围如下：
1 <= n , m <= 106, 1 <= x <= n+m，且a[1….n],b[1….m]中的数字在int范围内，且均为非降序列。
请完成以下判断题和选择题。
判断题：
1）给定任意合法输入，数组不会越界。（）
A. 正确
B. 错误
2）第23行代码的while更换成if不会对结果产生影响。（）
A. 正确
B. 错误
选择题
3）若输入以下数据，则输出为（）。
3 5 1
1 1 1
2 2 2 2 2
A. 5
B. 3
C. 8
D. 2
4）若输入以下数据，则输出为（）。
10 20 6
1 1 1 2 2 8 9 10 10000 1000000
4 4 4 4 4 5 8 8 8 8 10000 10000 10000 10000 10000 1000000 1000000 1000000 1000000 1000000
A. 23
B. 24
C. 25
D. 26
5）本题复杂度为（）。
A. O(n * m +x)
B. O(n * m * x)
C. O(n + m + x)
D. O((n + m) * x)
6）对于任意合法输入，ans最大可达到（）。
A. 2 * 106
B. 106
C. 231 – 1
D. 109
完善程序一：题意：给定 long long 范围内正整数 p 和 int 范围内正整数 q(q < p) 。求能整除 p （p%x==0），不能被 q 整除（x%q!=0）的最大整数 x。共询问 t 次。 
①处应填（）
A. p % q != 0
B. p == q
C. p % q == 0
D. p > q
②处应填（）
A. i * i < tq
B. i <= tp / i
C. i * i < tp
D. i <= tq / i
③处应填（）
A. while (tq % i == 0)
B. if (tq % i == 0)
C. while (i % tq == 0)
D. if (i % 2 == 0)
④处应填（）
A. while (tp % q == 0)
B. if (tp % q == 0)
C. while (tp % i == 0)
D. if (tp % i == 0)
⑤处应填（）
A. tp /= a[i]
B. tp /= q
C. tp /= i
D. tp = q * i
完善程序二：
有一棵结点数为n(n <= 1000)的严格二叉树，n称作这棵二叉树的大小，且二叉树的每个非叶子结点都恰好有两个子结点。为每个结点分配一个权值来表示以这个结点为根的子树的大小，然后按照先序遍历的思想把结点的权值列出作为它的特征序列。为了简化，只列出根节点和所有左子结点权值作为特征序列。经过观察，通过这样构造出的特征序列可以唯一确定一棵二叉树。现在给定一棵二叉树的特征序列，请还原出完整的二叉树的先序遍历结果，输入的特征序列保证题目有解。
输入样例：
7
13 7 1 3 1 1 1
输出样例：
13 7 1 5 3 1 1 1 5 1 3 1 1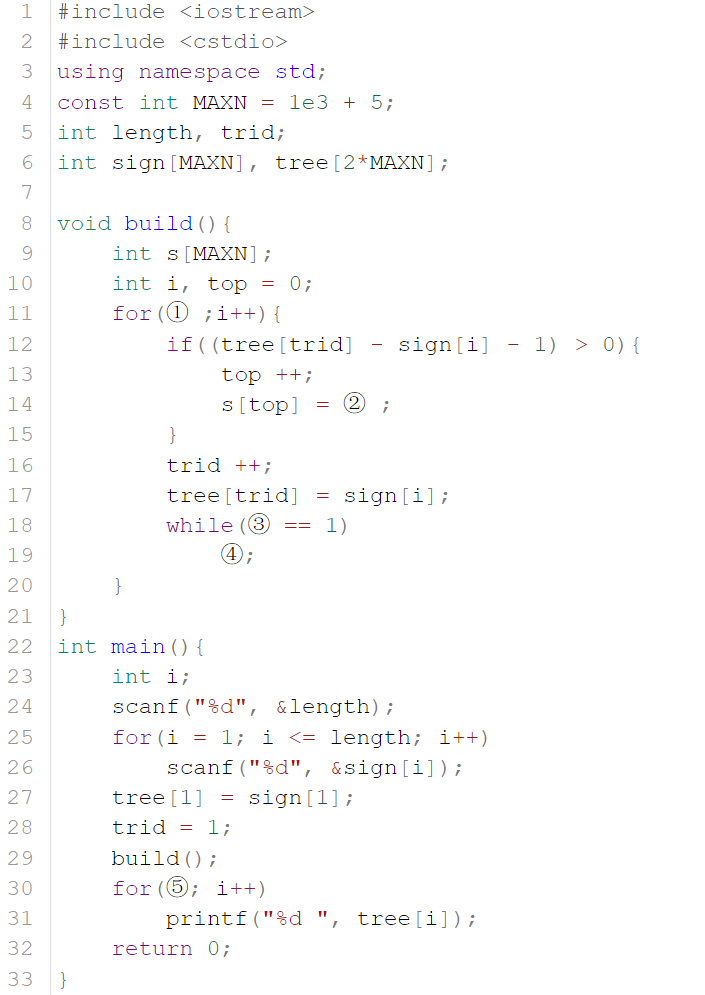
请完成下列的单选题：
①处应该填（ ）
A. i = 0; i < length
B. i = 1; i < length
C. i = 1; i <= length
D. i = 2; i <= length
②处应该填（ ）
A. tree[trid] – sign[i] – 1
B. tree[trid] – sign[i]
C. sign[i] – tree[trid] – 1
D. sign[i] – tree[trid]
③处应该填（ ）
A. s[top]
B. tree[trid]
C. sign[i]
D. tree[trid] – sign[i]
④处应该填（ ）
A. tree[trid++] = s[top–]
B. tree[++trid] = s[top–]
C. s[++top] = tree[–trid]
D. s[top++] = tree[trid–]
⑤处应该填（ ）
A. i = 0; i <= trid – 1
B. i = 0; i <= trid
C. i = 1; i <= trid – 1
D. i = 1; i <= trid