(1) 使用数组下标直接标记元素
哈希表(也叫散列表)：是一种高效的、通过把关键码值映射到表中一个位置来访问记 录的数据结构。
类似字符串，查找的时间复杂度是常数时间，缺点是，需要消耗更多的内存。
现在要存储和使用下面的线性表：A(12,83,284,49,183,13491,58)。
为了用0(1)的时间实现查找，可以开一个一维数组A[l… 13491],使得A[key]=key, 但显然造成了空间上的很大浪费，尤其是数据范围很大时。
(2) 除余法构造哈希值
为了使空间开销减少，我们可以对第二种方法加以优化，设计一个哈希函数H(key)= key mod 17，然后令A[H(key) ]=key,这样一来定义一个一维数组A[0.. .16]就己足够， 这种方法就是哈希表。
但这样会造成哈希冲突，比如：H(2)和H(19)的值都是2。
这里与字符串Hash有所不同，可能不论我们怎样选用哈希函数，还是很难避免产生冲突。
因此我们考虑对每一个哈希值记一个链表(其实也就相当于邻接表)，把所有等于同一 个哈希值的数字都存储下来，而查询只要遍历对应的链表即可，这样实际复杂度取决于查询的链表长度，也可以看做是常数级。
例如：我们定义哈希函数 H(x) = x mod 16,对数组 A(12,83,284,49,183,13491,58) 进行哈希运算后，插入一些数据的效果如下图。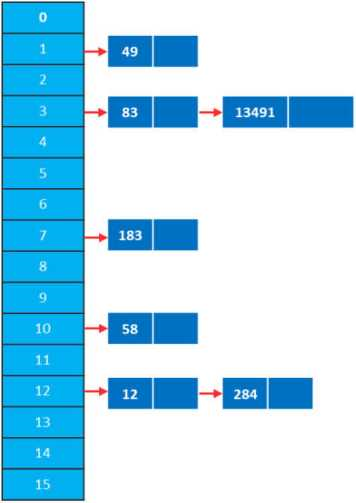
(3) 哈希函数的构造
取余法构造哈希：H(key) = key % b,为了尽量避免冲突，一般选为能够存储下并且尽量大的素数(一般情况下我们根据空间取106左右的素数，比如1000003，注意不要超过N)。一般地说，如果b的约数越多，那么冲突的几率就越大。
(4)哈希表主要有两个基本操作：
1.计算Hash函数的值；
2.定位到对应链表中依次遍历、比较。
无论是检查任意一个给点的原始信息在 Hash 表中是否存在，还是更新它在 Hash 表中的统计数据，都需要基于这两个基本操作进行。
分类