二叉查找树(Binary Search Tree,简称BST)它是具有下列性质的二叉树:
- (1) 树中每个结点被赋予了一个权值;(下面假设不同结点的权值互不相同)
- (2) 若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- (3) 若右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- (4) 左、右子树也分别为二叉查找树。

二叉查找树能够支持多种动态集合操作,只要所维护的数据集合存在大小关系。因此,它可以被用来表示有序集合、建立索引或优先队列等。我们也常常利用它动态地维护一个有序数集,利用二叉查找树找到新加入序列中的数插入的位置。
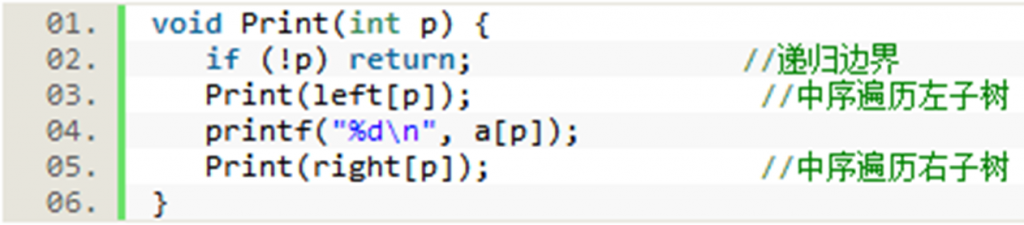
二叉查找树的遍历:
•对于一个已知的二叉查找树,从小到大输出其节点的值,只需对其进行二叉树的中序遍历,即递归地先输出其左子树,再输出其本身,然后输出其右子树。遍历的时间复杂度为O(n)。
二叉查找树的查找:
•对于一个已知的二叉查找树,在其中查找特定的值,方法如下:
(1) 从根节点开始查找;
(2) 如果当前节点的值就是要查找的值,查找成功;
(3) 如果要查找的值小于当前节点的值,在左子树中;
(4) 如果要查找的值大于当前节点的值,在右子树中;
(5) 如果当前节点为空节点,查找失败,二叉查找树中没有要查找的值。

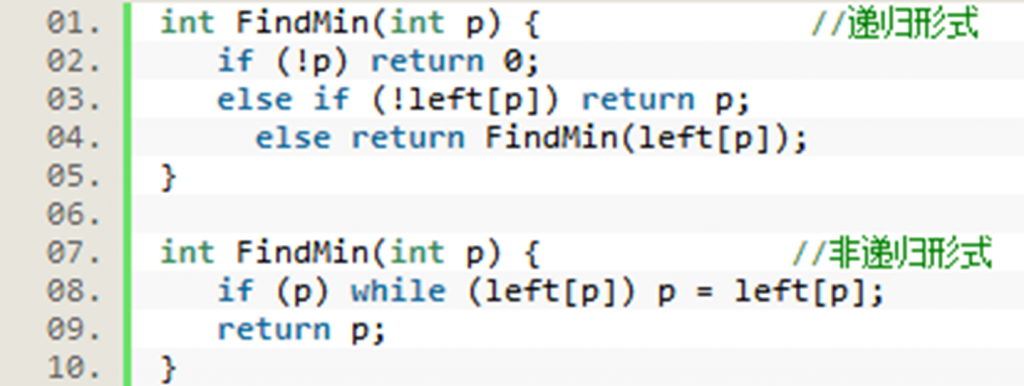
二叉查找树的查找最值:
•以最小值为例,从子树的根节点开始,如果左子节点不为空,那么就访问左子节点,否则当前节点就是该子树的最小值节点。
在二叉查找树中插入结点:
•在二叉查找树中插入元素,基本方法是类似于线性表中的二分查找,不断地在树中缩小范围定位,最终找到一个合适的位置插入。具体方法如下所述:
(1) 从根节点开始插入;
(2) 如果要插入的值小于当前节点的值,在当前节点的左子树中插入;
(3) 如果要插入的值大于当前节点的值,在当前节点的右子树中插入;
(4) 如果当前节点为空节点,在此建立新的节点,该节点的值为要插入的值,左右子树为空。
(5) 对于相同的元素,一种方法我们规定把它插入左边,另一种方法是我们在节点上再加一个域,记录重复节点的个数。

在二叉查找树中删除结点:
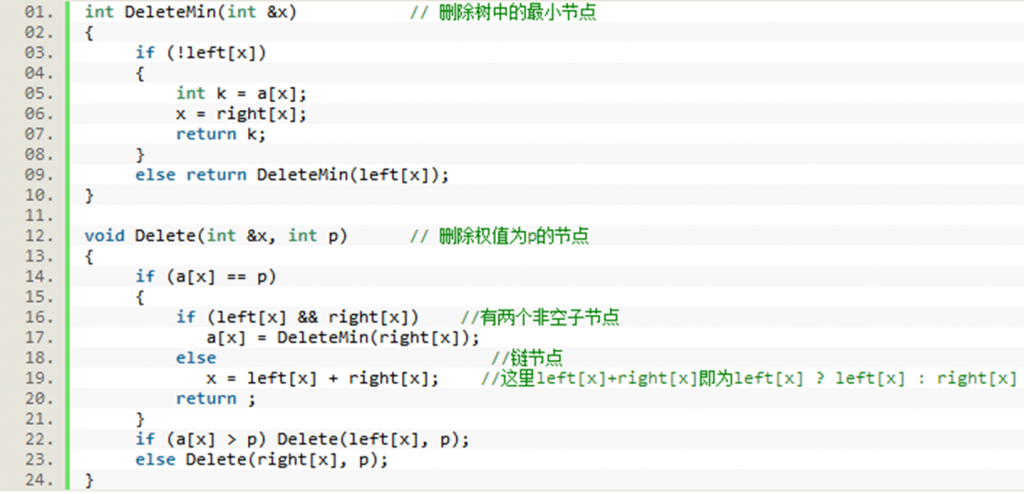
•二叉查找树的删除,基本方法是要先在二叉查找树中找到要删除的节点的位置,然后根据节点分为以下情况:
•情况一:该节点是叶节点(没有子节点的节点)。直接把节点删除即可。
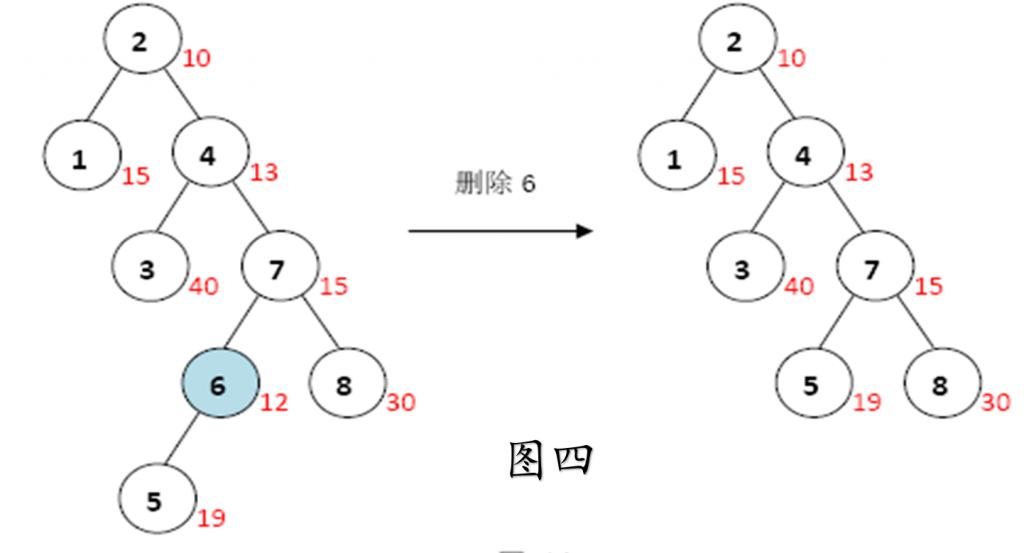
•情况二:该节点是链节点(只有一个子节点的节点)。则需要用它的子节点代替它的位置,然后把它删除。(如下图)
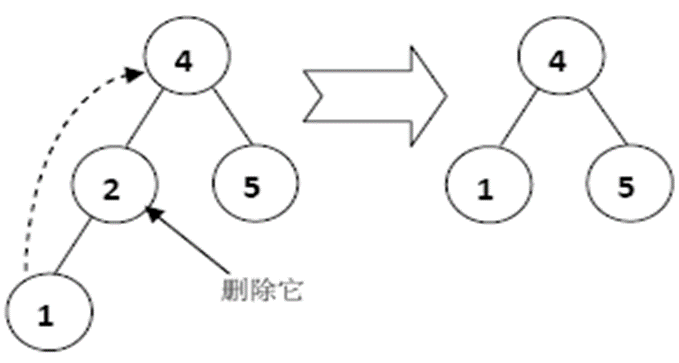
•情况三:该节点有两个非空子节点。由于情况比较复杂,一般的策略是用它右子树的最小值来代替它,然后把它删除。(如下图)
•实际上在实现的时候,情况一和情况二是可以一样对待的。而对待情况三除了可以用后继代替本身以外,我们还可以使用它的前驱(左子树的最大值)代替它本身。

优化:
•以上操作的时间复杂度都依赖于树的高度。
•实际上对于同样的结点集合,二叉查找树的形态并不唯一。在最好情况下单次操作的期望时间复杂度为 ;而最坏情况下,所有结点将会形成一条链(如右图),那么单次操作的复杂度将能达到 。
•而对二叉查找树进行改进,使得动态操作下,每种操作的最坏情况、期望或平摊的时间复杂度为 ,这样的二叉查找树就被称为平衡树。大部分的平衡树,如Treap,Splay等的平衡维护,都基于旋转操作。

•Treap是一种编写较为简单的平衡树,它在普通二叉查找树的基础上,给每个结点多赋予了一个属性:优先级。
•对于Treap中的每个结点,除了它的权值满足二叉查找树的性质外,它的优先级还满足小根堆性质。即从权值上看,Treap是一个二叉查找树;从优先级上看,Treap是一个堆。所以我们发现Treap其实可以看做是Tree+Heap。
•我们发现普通BST会不平衡是因为有序的数据会使查找路径退化成链,而随机数据使其退化的概率非常小。
•如果我们假设所有点的权值与优先级都互不相同,那么Treap的形态是唯一确定的。
•考虑在所有结点中找到优先级最小的点,则它一定是Treap的根,而权值小于它的点会在根的左子树,大于它的点会在根的右子树,这就可以递归下去构建Treap。这个建立过程与快速排序类似,因此Treap的期望深度与快排的递归层数一样都是期望的O(logn) 。
旋转(Zig/Zag)操作:
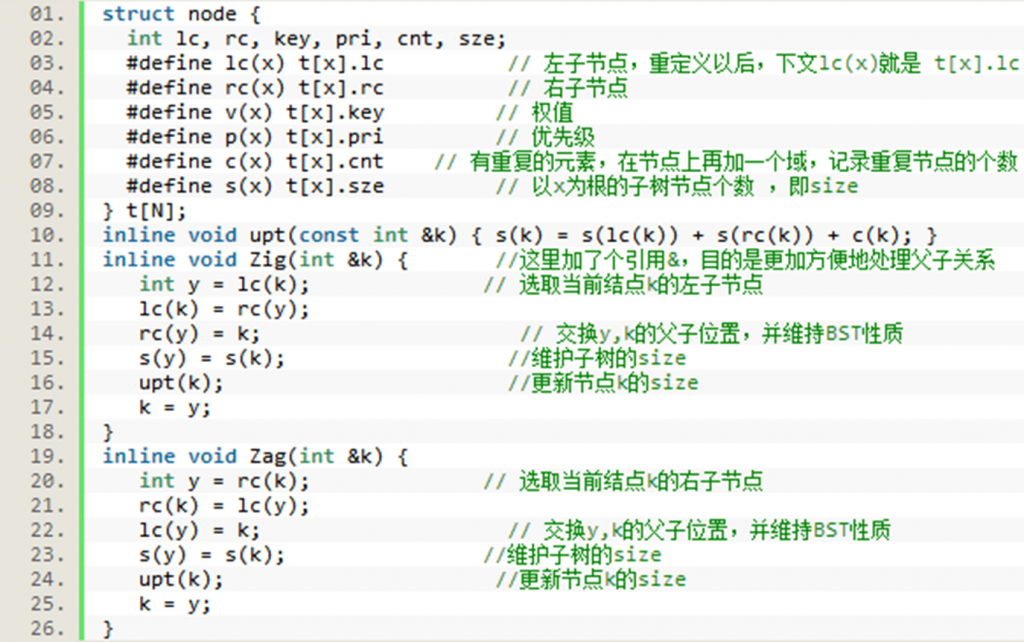
•为了使Treap同时满足BST性质和小根堆性质,有时要利用旋转对结构进行调整。在维护Treap的过程中,我们会出现两种旋转:左旋(Zig)与右旋(Zag):
(1) 左旋一个根节点为x的子树,则旋转后会把x变为这个子树的新根的左子节点,x的右子节点会成为子树新的根。
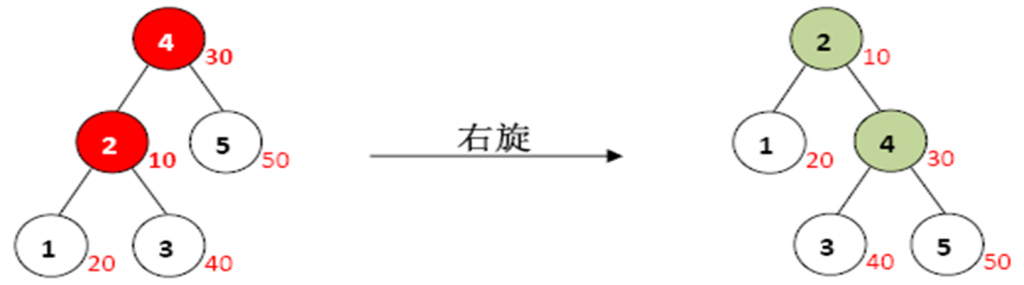
(2) 右旋一个根节点为x的子树,则旋转后会把x变为这个子树的新根的右子节点,x的左子节点会成为子树新的根。(如下图)

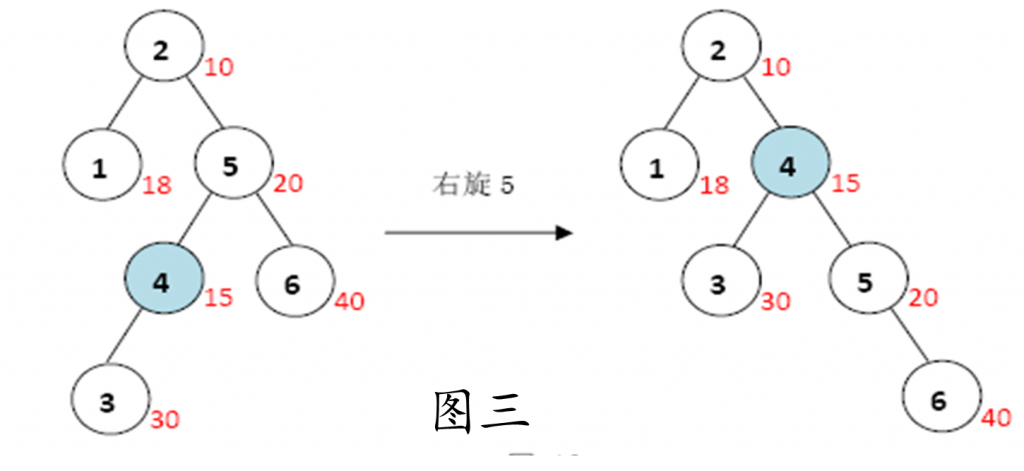
•显然旋转后Treap仍然满足权值的BST性质,而原本不满足堆性质的部分也通过旋转,使其满足堆性质。(旋转的意义:使不满足堆序的两个节点通过调整位置,重新满足堆序,而不改变BST性质。)举个例子:
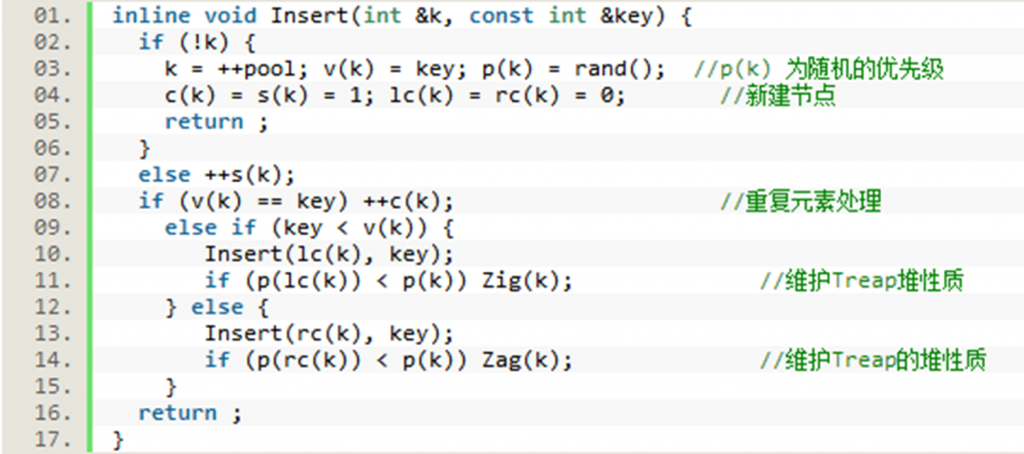
Treap插入操作:
•首先找到合适的插入位置,然后建立新的节点,存储元素。注意建立新的节点的过程中,随机生成的修正值(优先级)可能会破坏堆序,因此要进行恰当的旋转:
(1) 从根节点开始插入;
(2) 若该值小于等于当前节点的值,就往左子树中插入
(3) 若该值大于当前节点的值,就往右子树中插入
(4) 若当前节点为空节点,在此建立新的节点,新节点的值为该值,并随机生成一个优先级。注意在回溯时,要根据需要进行恰当的旋转。
(5) 插入后若左子节点的优先级小于当前节点的优先级,对当前节点进行右旋;
(6) 插入后若右子节点的优先级小于当前节点的优先级,对当前节点进行左旋;
Treap删除操作:
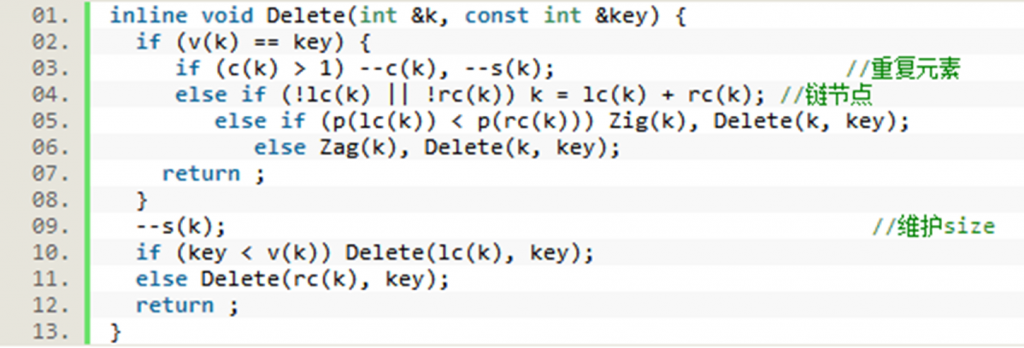
•首先要在Treap树中找到待删除节点的位置,然后分情况讨论:
情况一:该节点为叶节点或链节点,则该节点是可以直接删除的节点。若该节点有非空子节点,用非空子节点代替该节点的,否则用空节点代替该节点,然后删除该节点。
情况二:该节点有两个非空子节点。我们的策略是通过旋转,使该节点变为可以直接删除的节点。
求一个元素在Treap中的前驱/后继:(此处以求前驱为例)
•求一个元素在平衡树(或子树)中的前驱,定义为查找该元素在平衡树中不大于该元素的最大元素:
(1)从根节点开始访问,初始化最优节点为空节点;
(2)如果当前节点的值不大于要求前驱的元素的值,更新最优节点为当前节点,访问当前节点的右子节点;
(3)如果当前节点的值大于要求前驱的元素的值,访问当前节点的左子节点;
(4)如果当前节点是空节点,查找结束,最优节点就是要求的前驱。

在Treap中查找排名第k的元素:
•要维护以每个节点为根的子树的大小,用分而治之的思想来查找排名第k的元素。
•首先,在一个子树中,根节点P的排名是一个闭区间:

。在此基础上总结出算法:
(1)如果查找排名第k的元素(k∈A),则要查找的元素就是P所包含元素。
(2)如果
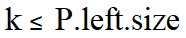
,则排名第k的元素一定在左子树中,且它在左子树中的排名第k。
(3)如果
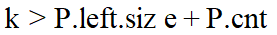
,则排名第k的元素一定在右子树中,且它在右子树中的排名第

。
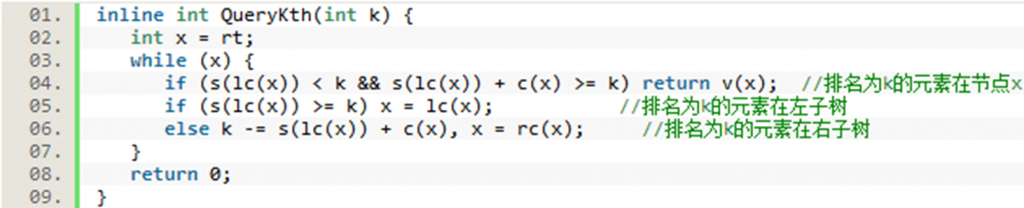
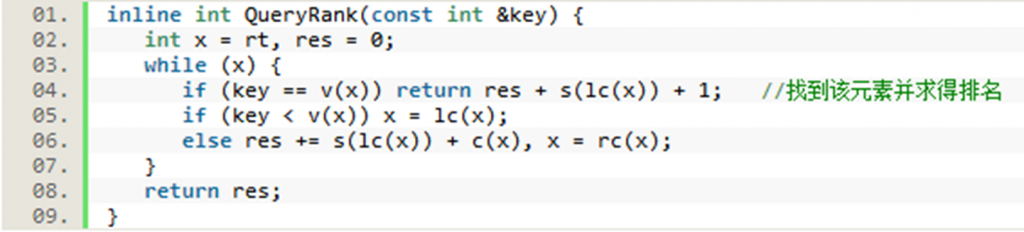
在Treap中求元素的排名:
•规定,如果在Treap中有多个重复的元素,则这个元素的排名为最小的排名。(例:1,2,4,4,4,6)。在Treap中求元素的排名与查找第k小的数是相似的。
•基本思想是查找该元素在Treap中的位置,同时统计出小于该元素的节点的总个数,则该元素的排名就是总个数+1。算法为:
(1)定义P为当前访问的节点,res为当前已知的比该元素小的元素个数。初始化res为0;
(2)若该元素等于当前节点元素,则该元素的排名为P.left.size + res + 1;
(3)若该元素小于当前节点元素,往左子树中查找;
(4)若该元素大于当前节点元素,往右子树中查找,并更新res为res + P.left.size + P.cnt。