一、强连通图 在有向图中,任意两个顶点互相可达。
强连通分量 在有向图中,极大的强连通子图。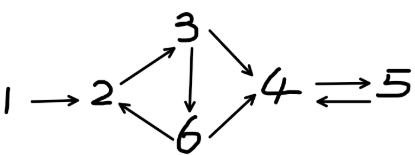
我们需要求出如下信息:
1)、有几个强连通分量,他们的编号分别是几?
2)、每个强连通分量分别有几个点?
3)、每个点属于哪个强连通分量?
二、Tarjan算法 是基于对图深度优先搜索(DFS)的算法,每个强连通分量为搜索树中的一棵子树。搜索时,把当前搜索树中未处理的结点加入一个栈,回溯时可以判断栈顶到栈中的结点是否为一个强连通分量。具体操作:
1、主要数组和变量
dfn[i]:编号点i的时间戳(时间序)
low[i]:编号点i能访问到的最小时间序
id[i]:点i所属的SCC编号;
si[t]:编号为t的SCC内部有几个点
stack st:走过的,但没有被去除的强连通分量SCC的点;
bool v[i]:标记i点是否在栈中
cnt: 当前的SCC总数量 (包括1个元素的SCC)
ans:元素个数大于1的SCC的数量 2、求解原理
2、求解原理
(1). 走到每个点,将该点的时间序和最小能访问到的时间序设为++step;
dfn[x]=low[x]=++step;
(2). 遍历x所有邻边,假设要去的邻点为to,考虑两种情况
❶、to点没有被访问过:深搜去to点,从to点后退时 low[x]=min(low[x],low[to]);
❷、to点已经被访问过,且to还在栈中,说明to所属的SCC还没有被取出来 low[x]=min(low[x],dfn[to]);
(3). 从x后退,判断x是否是SCC的入口(即low[x]==dfn[x]),如果是,从栈顶开始弹出SCC的所有元素,一直到x,x也要被弹出,将这些元素统计到同一个强连通分量中。
3、时间复杂度 Tarjan算法的过程中,每个顶点都被访问了一次,且只进出了一次栈,每条边也只被访问了一次,所以该算法的时间复杂度为O(n+m)。(n表示点数,m表示边数)
三、Tarjan与缩点
什么是缩点 缩点是一种图论算法,用于将有向图的强连通分量缩成一个结点,并构造一个新的有向无环图(DAG)。这个新的图中的每个结点代表原图的一个强连通分量。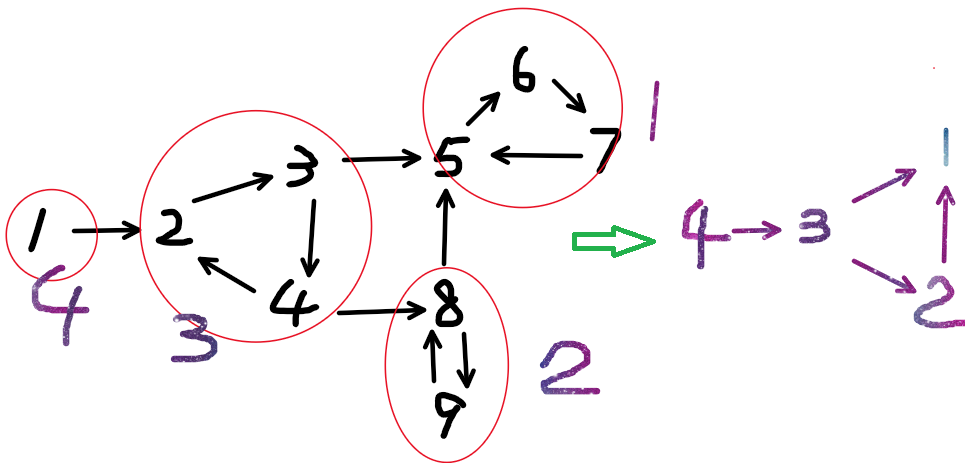
所有能走到点x的那些点,在拓扑排序中,一定是出现在点x之前的。因此拓扑排序的结果,是满足DP中的无后效性的。
f[i]:以点i结尾的经过数字和的最大值。
边界:如果rd[i]==0,说明点i不受其他点的影响,则f[i]=w[i]。
状态转移方程:f[to]=max(f[to],f[x]+w[to]);
如果x点出队了,用点x的最优解,更新x能走到的to的最优解。
最终目标答案:max(f[i])。
四、有向无环图( DAG )有许多重要的性质
1.拓扑排序: DAG 可以进行拓扑排序,即按顺序列出所有顶点。这可以用于寻找依赖关系,或确定执行顺序。
2.单源最短路径: DAG 上可以使用拓扑排序和动态规划计算单源最短路径。
3.DAG上必然存在出度、入度为0的结点。
4.DAG上若存在唯一出度为0的结点,则该结点可被 DAG 上其他所有结点到达。
5.问在 DAG 上最少选择多少个点能够使得从这些点出发可以到达所有点,那么答案就是入度为0的点的个数。
6.假设 DAG 上出度为0的结点有 a 个,入度为0的结点有 b 个,那么再加 max(a,b)条边可以使得该有向图强连通。
