一、差分约束 是一种特殊的N元一次不等式组。它包含N个变量x1~xN以及M个约束条件,每个约束条件都是由两个其中的变量作差构成的,形如xi-xj>=ck,其中ck是常数(可正可负)且1<=i,j<=N, 1<=k<=M。
我们要解决的问题就是:求一组解 x1=a1,x2=a2,…,xN=aN,使所有约束条件都得到满足,否则判断出无解。
举例:
x1-x2≤3
x3-x2≤2
x1-x3≤1
则:x1=4,x2=3,x3=5,就是满足差分约束的一组解,由于将x1…xn加上同样的常数t,依然能使得所有的不等式满足,因此不等式的解并不唯一。
二、如何计算差分约束的可行解?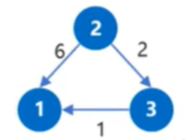
设有如图所示的有向图,如果求出从源点s到每个点i的最短路x[i]之后,必定满足:
x[1]≤x[2]+6
x[3]≤x[2]+2
x[1]≤x[3]+1
也就是,如果图中存在一条从i点指向j点的长度为c的有向边,设到i点的最短路为xi,到j点的最短路为xj,则必定满足三角不等式:xj≤xi+c。
第一步:转换为图论问题
因此,可以将差分约束的不等式转换为:从i点指向j点的长度为c的有向边,从图中选一个源点s,求出s到每个点的最短路。
第二步:选择源点s
由于需要满足所有的不等式,因此需要满足:所有的边在图中都一定要能遍历到,也就是说,图中的源点s必须满足:从s出发能遍历到每一条边。如果图中不存在满足要求的源点,则:建虚拟源点s’使得s’到每个点都有一条边。
第三步:计算
(1):最短路计算
由于差分约束描述的是相对关系,因此仅仅靠不等式是无法求解的,还需要一个“绝对的值”才能计算。比如,如上所示的图中,假设取2为源点,且x[2]=0,那么如果要求其余xi的最大值。
则需要满足:
x[1]≤x[2]+6≤6
x[3]≤x[2]+2≤2
x[1]≤x[3]+1≤x[2]+2+1≤3
且x[3]最大取2,而x[1]要同时满足x[1]≤6&&x[1]≤3,那么x[1]只能取3。对应到图论,相当于2点到1点有两条路,x[1]要取两条路的最小值。
因此,有结论如下:如果要求xi的最大值,则转换为最短路问题;相反的,如果要求xi的最小值,则转换为最长路问题。
注意:如果仅有不等式xi≤k,则可以视为xi≤x0+k,x0为虚拟点,也即是虚拟点x0到点xi之间存在一条长度为k的边。
(2):最长路计算
上述三角不等式如果要求最小值,则可以先将式子转换为≥的形式如下:
x[2]≥x[1]-6
x[2]≥x[3]-2
x[3]≥x[1]-1
也就是,如果图中存在一条从i点指向j点的长度为c的有向边,设到i点的最长路为xi,到j点的最长路为xj,则必定满足三角不等式:xj≥xi+c。
将上述三角不等式组转换为下面这张图,可以取点1为源点(点1可以经过所有的边),并假设点1的值为0,求点2和点3的最小值。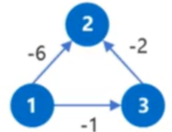
x[2]≥x[1]-6≥-6
x[3]≥x[1]-1≥-1
x[2]≥x[3]-2≥x[1]-1-2≥-3
则:x[3]最小值取-1,而x[2]要同时满足x[2]≥-6&&x[2]≥-3,那么x[2]只能取-3。
(3)差分约束无解的情况
既然是求从源点s到每个点的最短路,因此如果从s出发可以走出负环,则差分约束无解。同理,求最长路,如果存在正环,则差分约束无解。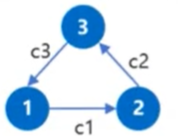
以最短路为例,如图所示,假设从点1出发走出负环,则意味着c1+c2+c3<0,到每个点的最短路满足:
x[2]≤x[1]+c1 [式1]
x[3]≤x[2]+c2 [式2]
x[1]≤x[3]+c3 [式3]
将式2代入式3可得:x[1]≤x[2]+c2+c3,再将式1代入可以得:x[1]≤x[1]+c1+c2+c3,因为c1+c2+c3<0,所以不等式无解。
