一、双向广搜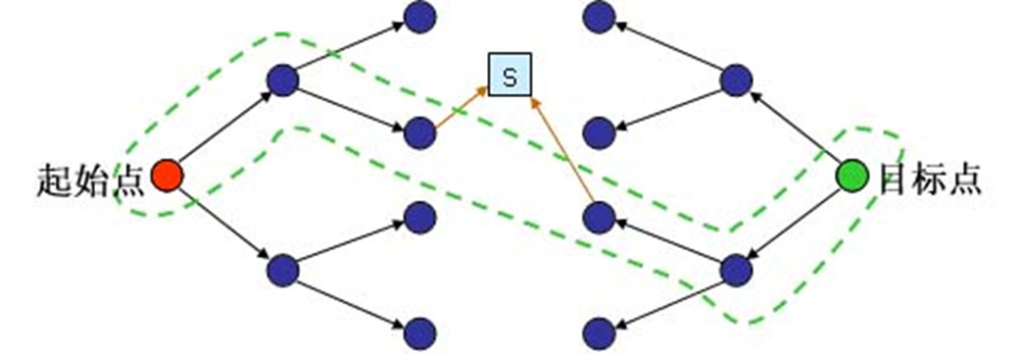
从正反两个方向进行宽度优先搜索，可以大大减少搜索量，提高搜索速度。从初始状态和目标状态两个方向同时进行扩展，如果两棵解答树在某个节点第一次发生重合，即可终止此搜索过程，则该节点所连接的两条路径所拼成的路径就是最优解。双向宽度优先搜索通常有两种搜索方法：
①两个方向交替扩展；
②选择结点个数较少的那个方向先扩展。
方法2只需要略微修改一下控制结构，每次while循环时只扩展正反两个方向中节点数目较少的一个，可以使两边的发展速度保持一定的平衡，从而减少总扩展节点的个数，加快搜索速度。
很明显，方法2优于方法1。
算法说明：
①设置两个队列q[2][maxn]，分别表示正向和逆向的扩展队列。
②设置两个头指针l[2]分别表示正向和逆向将扩展结点的头指针。
③设置两个尾指针r[2]分别表示正向和逆向的尾指针。
二、双端队列BFS算法思想
釆用BFS直接求最少步数的前提：图中所有点之间的边权是相等的。在图论问题中有一种特例：边权的值不是0就是1,可以称之为01模型求最短路。
由于这是一张边权要么为0要么为1的图。在这样的图上，我们可以通过双端队列广搜来计算。
算法的整体框架与一般的广搜类似，只是在每个节点沿分支拓展时稍作改变。如果这条分支边权为0，则从队首入队，否则从队尾入队。
这样我们能保证，任意时刻广搜队列中节点对应的距离值都有：
(1) “两段性”(队列中最多存在两段，到第一段的每个点的步数为step，到第二段每个点的步数为step+1)；
(2) “单调性”(队列中走到每个点的步数具有单调性),每个结点第一次出队时，就能得到最短距离。
我们可以知道该算法中每个节点仅被访问一次，因为这是BFS的特性，所以该算法的效率为O(N)。
双端队列BFS的注意事项：双端队列BFS求最短路时，并不是走到就是最短路，而是在该点第一次岀队时, 才能求得最短路。
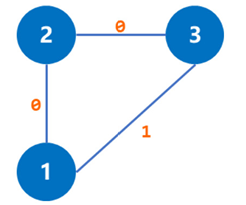
比如：如图所示，求从1点到3点的最短路，显然是0，而不是1。