KMP算法

KMP算法 是一种改进的字符串匹配算法，由 D.E.Knuth, 3.H.Morris 和 V.R.Pratt 提出的，因此人们称它为克努特一莫里斯一普拉特操作(简称KMP算法)。
KMP算法的核心 是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现，函数本身包含了模式串的局部匹配信息。
KMP算法的时间复杂度O(m+n)。

1、KMP的原理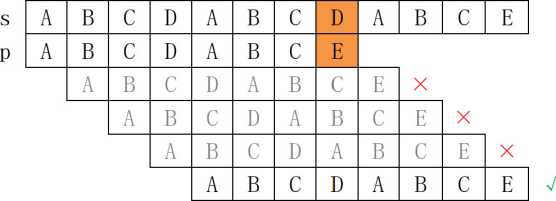

如：有上图所示的父串s和子串p,如果要匹配出子串p在父串s中是否出现过或者出 现过多少次。
暴力的做法如图所示，第1次父串s从第1个字符开始和子串匹配，匹配到第8个字 符发现不等，匹配失败。
第2次父串s从第2个字符开始尝试和子串匹配，由第1次匹配可知，s[2]= ‘B’，而 t1 = ‘A’, 显然匹配不成功。第3次从s的第3个字符开始尝试和子串p匹配……
如果s的长度为n, p的长度为m, 则：暴力求解的时间复杂度是O(n*m)_o

问题：能否直接跳过中间肯定失败的3次匹配呢？
回答：答案是肯定的，因为第1次匹配，发现s[8] != p[8]时，观察p的前7个字符 发现，p有3个前缀子串和3个后缀子串完全匹配，可以利用这个性质，直接跳过中间的3次无效的匹配。

2、next数组的计算方法
(1)  加快匹配的原理 上述案例中，我们使用 i 来循环 s 主串，j 循环 p 子串，我们希望：s 主串的 [i-j+1,i] 字符和 p 子串的 [1,j] 字符完全一致，也就是 s 串以 s[i] 结尾的长度为 j 的子串和 p 字符串的前 j 个字符一致，显然样例可以分析出 i=7、j=7 时是能做到的，接下来检验 s[i+1] 和 p[j+1] 的关系。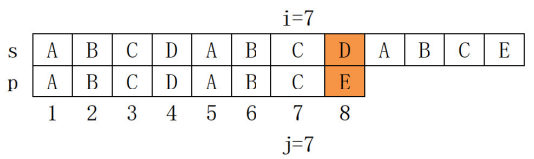

由于 s[8] != p[8] 此时 i 和 j 无法继续增加，要尝试继续匹配，必须减少 j,且为 了提升效率，新的 j 越大越好。因为p[1. .3]==p[5..6],因此新的 j 最大可以设置为3, 到下图所示的状态，重新检验 s[i+1] 和 p[j+1] 的关系。

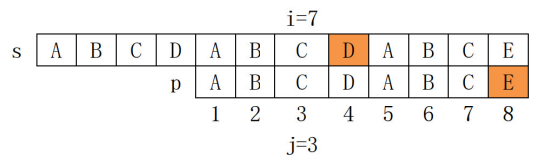当发现 s[i+1] != p[j+1] 时，j 的最大可以回跳的值 == p字符串1..j 这 j 个字符前缀和后缀相等的最大长度。
(1)   next数组的含义 next[j] 代表字符串 p 中前 i 个字符的最大相同前缀和后缀的值。特别注意：这个值不含自身，比如字符串 “ABABA” 最大相同前缀和后缀的值是3, 而不是5, 因为任何字符串如果取自身，那么从前缀和后缀必定相等。因此next[0] = next[1] =0 。
(2)   如何高效匹配
当 s[i+1] != p[j+1], 通过 j=next[j] 回跳，如果 s[i+1] == p[j+1], 那么往后继续匹配。(注意：为了避免next和系统函数同名，一般 next 数组定义时可以使用缩写 ne )
(3)   如何高效求next数组
类似字符串 s 和 p 匹配的过程，只是求 p 的 next 数组本质上是 p 自己和自己匹配的过 程。