1957年理查德·贝尔曼在《Dynamic Programming》一书中提出的一种表格处理方法，它把原问题分解为若干子问题，自底向上先求解最小的子问题，把结果存储在表格中，求解大的子问题时直接从表格中查询小的子问题的解，以避免重复计算，从而提高效率。
一、什么是动态规划 每次决策依赖于当前状态，又随即引起状态的转移。一个决策序列就是在变化的状态中产生出来的，这种多阶段最优化决策解决问题的过程就称为动态规划。
动态规划(Dynamic Programming)算法是解决多阶段决策过程最优的通用方法。在这类问题中，可能会有许多可行解。每一个解都对应于一个值，我们希望找到具有最优值的解。要了解动态规划的概念，首先要知道什么是多阶段决策问题。
二、多阶段决策问题
如果一类活动过程可以分为若干个互相联系的阶段，在每一个阶段都需作出决策(采取措施)，一个阶段的决策确定以后，常常影响到下一个阶段的决策，从而就完全确定了一个过程的活动路线，则称它为多阶段决策问题。
各个阶段的决策构成一个决策序列，称为一个策略。每一个阶段都有若干个决策可供选择，因而就有许多策略供我们选取，对应于一个策略可以确定活动的效果，这个效果可以用数量来确定。策略不同，效果也不同，多阶段决策问题，就是要在可以选择的那些策略中间，选取一个最优策略，使在预定的标准下达到最好的效果。
例子：城市交通路网 http://oj.lizi101.com/problem.php?id=1310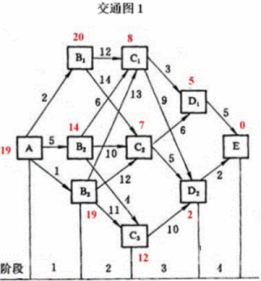
思考：仔细观察本图路径的特殊性，可以分成4个阶段:
第一阶段：A有三条路，分别到B1、B2、B3；
第二阶段：B1有两条路通……；B2有三条通路……；B3有三条路通…..
三、3个基本概念
1、 阶段 问题的过程被分成若干相互联系的部分，我们成为阶段，以便按一定的次序求解。
2、 状态 某一阶段的出发位置称为状态,通常一个阶段包含若干状态，如第3层有 dp(C1)、dp(C2)、dp(C3)、dp(C4) 状态。
3、 决策 对问题的处理中作出的每种选择的行动就是决策。即从该阶段的每个状态出发，通过一 次选择性的行动移至下一个阶段的相应状态。
四、问题的解决步骤
动态规划所处理的问题是一个多阶段决策问题，一般由初始状态开始，通过对中间阶段决策的选择，达到结束状态。这些决策形成了一个决策序列，同时确定了完成整个过程的一条活动路线(通常是求最优的活动路线)。如图所示。动态规划的设计都有着一定的模式，一般要经历以下几个步骤：初始状态→│决策１│→│决策２│→…→│决策ｎ│→结束状态
(1) 将原问题分解为子问题：按照问题的时间或空间特征，把原来的问题分为若干个子问题，子问题和原问题形式相同或者类似。在划分子问题时，注意划分后的子问题的解决一定是有序的或者是可排序的，否则子问题就无法依次求解。子问题都解决了，原问题即解决。
以数字三角形：http://oj.lizi101.com/problem.php?id=1302 为例，子问题是一个数字它正下方到底边最大和 和它右下方到底边最大和，两个子问题都解决后，取个两个子问题中的最优解。一旦子问题得到解后，要将结果保存下来，以避免同一个子问题被多次计算。 重叠子问题：dp(1,1),dp(2,1),dp(2,2)……这些问题的共性：都是求从一个位置出发到底部的最大值；是一个共同的问题。 重叠子问题(overlapping subprob-lems)是动态规划展示威力的关键。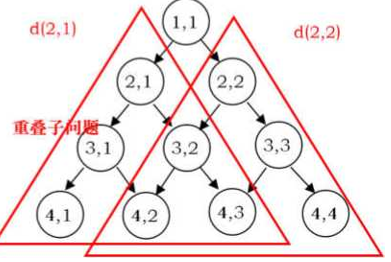
(2) 确定状态：在用动态规划解决问题时，往往将和子问题相关的各个变量的一组取值，称之为一个“状态”。一个“状态”对应于一个或者多个子问题，所谓某个“状态”下的“值”，就是这个“状态”所对应的子问题的解。
以数字三角形为例，子问题是一个数字它正下方到底边最大和 和它右下方到底边最大和，状态就是该数字的行号i和列号j，状态下的值就是行i列j到底边的最大和。
所谓“状态”的集合，构成问题的“状态空间”的大小，与用动态规划解决问题的时间复杂度直接相关。
在数字三角形例子里，一共有N*(N+1)/2个数字，所以这个问题的状态空间里一共就有N*(N+1)/2个状态。
整个问题的时间复杂是状态数目乘以计算每个状态所需要的时间。
在数字三角形例子里，每个“状态”都需要计算一次，且在每个状态上作计算所花的时间都是和N无关的常数。所以，时间复杂度是O（n2）。
用动态规划阶解题，经常碰到的情况是，K个整型变量能构成一个状态（如数字三角形的行号和列号，如会场教室安排的时间戳）。如果这K个整型变量的取值范围分别是n1,n2,…,nk,那么我们就可以用一个K维的数组array[n1] [n2] … [nk] 来存储各个状态的“值”。这个“值”未必就是一个整数或浮点数，可能是需要构成一个结构体才能表示的，那么array就可以是一个结构体数组。一个“状态”下的“值”通常回事一个或多个子问题的解。
(3) 确定一些初始状态的值（即边界状态的值）：
以数字三角形为例，初始状态就是底边数字，值就是底边数字值。
通过初始状态，推导其他状态的“值”，也就是已知推未知。
(4) 确定状态转移方程：前面已经定定义了什么是“状态”，以及该“状态”下的“值”的表示方式。现在就要找出不同的状态之间如何迁移—–就是如何从一个或多个已知的状态“值”，求出另一个“状态”的“值”（递推）。显然，状态的迁移可以用递推公式来表示，此递推公式可以被称作“状态转移方程”。
数字三角形a[i][j]的状态转移方程： maxSum[i][j]=a[i][j]; r=n (相当于边界，初始状态) maxSum[i][j]=max(maxSum[i+1][j],maxSum[i+1][j+1])+a[i][j]; r<n
五、能用动态规划解决的问题的特点
动态规划一般解决最值(最优，最大，最小，最长……. )问题；能采用动态规划求解的问题的一般要具有3个性质：
(1) 问题具有最优子结构的性质：如果问题的最优解所包含的子问题的解也是最优的，就称该问题具有最优子结构，即满足最优化原理。
(2) 无后效性：即某阶段状态一旦确定，就不受这个状态以后决策的影响。也就是说，某状态以后的过程不会影响以前的状态，只与当前状态有关。与当前状态得到的过程无关。
(3) 有重叠子问题：即子问题之间是不独立的，一个子问题在下一阶段决策中可能被多次使用到。动态规划算法利用此性质，对每个子问题只计算一次，然后将其结果保存起来以便高效重用。（该性质并不是动态规划适用的必要条件，但是如果没有这条性质，动态规划算法同其他算法相比就不具备优势）
使用动态规划的前提：能划分阶段、有最优子结构、无后效性。
六、算法实现的说明
动态规划的主要难点在于理论上的设计，也就是上面4个步骤的确定，一旦设计完成，实现部分就会非常简单。使用动态规划求解问题，最重要的就是确定动态规划三要素：
（1）问题的阶段
（2）每个阶段的状态
（3）从前一个阶段转化到后一个阶段之间的递推关系（决策）。
递推关系必须是从次小的问题开始到较大的问题之间的转化，从这个角度来说，动态规划往往可以用递归程序来实现，不过因为递推可以充分利用前面保存的子问题的解来减少重复计算，所以对于大规模问题来说，有递归不可比拟的优势，这也是动态规划算法的核心之处。
确定了动态规划的这三要素，整个求解过程就可以用一个最优决策表来描述，最优决策表是一个二维表，其中行表示决策的阶段，列表示问题状态，表格需要填写的数据一般对应此问题的在某个阶段某个状态下的最优值（如最短路径，最长公共子序列，最大价值等），填表的过程就是根据递推关系，从1行1列开始，以行或者列优先的顺序，依次填写表格，最后根据整个表格的数据通过简单的取舍或者运算求得问题的最优解。
动归的常用两种实现形式：
1）递归型 直观，容易编写。但可能会因递归层数太深导致爆栈，函数调用带来额外时间开销。无法使用滚动数组节省空间。总体来说，比递推型慢。使用记忆化搜索可以有效的减少重复计算。
2）递推型 效率高，有可能使用滚动数组节省空间。
七、穷举与动态规划
动态规划比穷举具有较少的计算次数。从数塔问题可以看岀，层数为k时：穷举算法求路径的条数：2k-1；动态规划计算的次数为：k*(k+1)/2。
八、分治与动态规划
相同点：将问题分解为子问题，然后合并子问题的解得到原问题的解。
不同点：分治的子问题不重叠。动态规划的问题拥有重叠子问题。
九、贪心与动态规划
相同点：要求原问题必须有最优子结构。
不同点：贪心法的计算方式“自顶向下”，但并不等待子问题求解完毕后再选择使用哪一个，而是通过一种策略直接选择一个子问题去求解，没被选择的子问题直接抛弃。这种所谓“最优选择”的正确性需要用归纳法证明。而动态规划不管是采用自底向上还是自顶向下的计算方式，都是从边界开始向上得到目标问题的解(即考虑所有子问题)。
贪心：壮士断腕的决策，只要选择，绝不后悔。
动态规划：要看哪个选择笑到最后，暂时领先说明不了问题。