Floyd 算法又称为插点法,是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法,与 Dijkstra 算法类似。该算法名称以创始人之一、1978 年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特 · 弗洛伊德命名。
状态转移方程: f[i,j]=min{f[i,k]+f[k,j],f[i,j]},注意:点k作为最外层循环。时间复杂度为 O(n3),
算法描述:
1. 从任意一条单边路径开始。所有两点之间的距离是边的权,如果两点之间没有边相连,则权为无穷大。
2. 对于每一对顶点 u 和 v,看看是否存在一个顶点 w (一般称为中间点)使得从 u 到 w 再到 v 比已知的路径更短。如果是,松弛它。
3. 遍历直到结束,这时候存储图的数据结构就得到了多源最短路径。
传递闭包 概念:给定一个集合,以及若干元素的传递关系,传递闭包问题是求解所有元素的联通关系,如给定集合 {a,b,c} ,已知 a->b,b->c,我们可以推出 a->c 。
如果是借已知单向图推两点间的联通关系,可以用 DFS 或 BFS, 复杂度为 O(n+m)。但是求解传递闭包问题时,我们需要求得所有点对之间的联通关系,复杂度就达到了 O(n*(n+m)) ,在稠密图中,复杂度约等于O(n3) ,这么高的复杂度,我们可以用相同复杂度但是代码简单的Floyd进行处理。
具体方案是用点对间的联通关系来代替原本的路径长度进行递推。
若 dp[i][k]=1 并且 dp[k][j]=1(等于 1 表示两节点联通),则说明节点i可以借由节点k到达节点j。
动态转移方程就变成了:dp[i][j] |= dp[i][k] & dp[k][j]
传递闭包的Floyd代码:
for(int k = 1; k <= n; ++k)
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= n; ++j)
dp[i][j] |= dp[i][k] & dp[k][j];简单优化一下:先判断 dp[i][k] 是否为 1 再进入 j 的循环,可以减少一点计算时间。
for(int k = 1; k <= n; ++k)
for(int i = 1; i <= n; ++i)
if(dp[i][k])
for(int j = 1; j <= n; ++j)
if(dp[k][j])
dp[i][j] = 1;复杂度还是 O(n3) 。但实际上这个代码还能再进行优化,因为 dp 数组中的值只有 0 和 1 。而且最后一层里,dp[k][j] 为 1 时将 dp[i][j] 赋值为 1 ,这个操作其实可以用或操作来取代。所以终极的优化就是使用 bitset ,既可以存 0、1,还可以直接进行位运算。 具体代码如下:
bitset<N> dp[N];
void Floyd(){
for(int k = 1; k <= n; ++k)
for(int i = 1; i <= n; ++i)
if(dp[i][k])
dp[i] |= dp[k];
}最后复杂度降为了 O(n2) ,优于直接搜索,可以处理 1000 的数据量。
🔍 核心知识要点一览
掌握 Floyd 算法,关键在于理解其作为“多源”最短路径算法的独特之处,特别是其基于动态规划的核心思想。
| 知识模块 | 关键知识点 | 说明与要点 |
|---|---|---|
| 核心思想 | 动态规划 (Dynamic Programming) | 通过逐步引入中间顶点,利用子问题的解来构建全局解。其精髓在于三层循环中的状态转移。 |
| 独特优势 | 多源最短路 (All Pairs Shortest Path) | 一次执行即可计算出图中任意两个顶点之间的最短路径。 |
| 关键操作 | 松弛操作 (Relaxation) | 检查对于顶点 i 和 j,是否存在一个中间顶点 k,使得路径 i → k → j 的距离小于当前已知的 i → j 距离,如果是则更新。 |
| 状态转移方程 | d[i][j] = min(d[i][j], d[i][k] + d[k][j]) | 这是算法的灵魂。k 是中间顶点,在循环中不断穷举。 |
| 数据结构 | 邻接矩阵 (Adjacency Matrix) | 使用二维数组 dist[][] 存储任意两点间的当前最短距离。初始化时,顶点到自身为0,有直接边则为权值,无直接边则为无穷大 (INF)。 |
| 时间复杂度 | O(∣V∣³) | 其中 ∣V∣ 是顶点数。源于三层嵌套循环。 |
| 空间复杂度 | O(∣V∣²) | 用于存储距离矩阵。可通过滚动数组技巧优化,将本需的三维DP数组降至二维。 |
| 负权边处理 | 可以处理 | 能够处理图中包含负权边的情况。 |
| 负权环检测 | 检查对角线 | 算法结束后,检查距离矩阵主对角线上的元素 dist[i][i]。如果存在某个值小于0,则说明图中存在从顶点 i 可达的负权环(负权回路)。 |
| 算法局限性 | 时间复杂度高 | 不适用于顶点数非常多的大规模图。 |
💡 动态规划思想与实现要点
Floyd算法的精妙之处在于其动态规划的本质。
- 状态定义:算法的基本状态可以定义为
d[k][i][j],表示只使用编号为 1 到 k 的顶点作为中间顶点时,顶点 i 到 j 的最短路径长度。 - 状态转移:对于
d[k][i][j],我们考虑是否要经过第 k 个顶点:- 不经过 k:那么最短路径长度等于只使用前 k-1 个顶点时的长度,即
d[k-1][i][j]。 - 经过 k:那么路径拆分为 i → k 和 k → j,长度之和为
d[k-1][i][k] + d[k-1][k][j]。
取这两种情况的最小值,就得到了状态转移方程:d[k][i][j] = min(d[k-1][i][j], d[k-1][i][k] + d[k-1][k][j])。
- 不经过 k:那么最短路径长度等于只使用前 k-1 个顶点时的长度,即
- 滚动数组优化:在实际编码中,我们可以发现
d[k]只依赖于d[k-1],因此可以省略第一个维度,利用一个二维数组进行“滚动”更新,这就得到了常用的形式:d[i][j] = min(d[i][j], d[i][k] + d[k][j])。关键在于,k 的循环必须放在最外层,这样才能保证在更新d[i][j]时,d[i][k]和d[k][j]已经是考虑过前 k-1 个中间顶点的最优解(即上一状态的值)。
⚖️ 对比与选型:何时选择Floyd?
了解一个算法的优缺点和适用场景,与理解其原理同等重要。为了帮助你更直观地理解Floyd在算法家族中的位置,以及如何在具体问题中做出选择,可以参考下面的决策流程图:
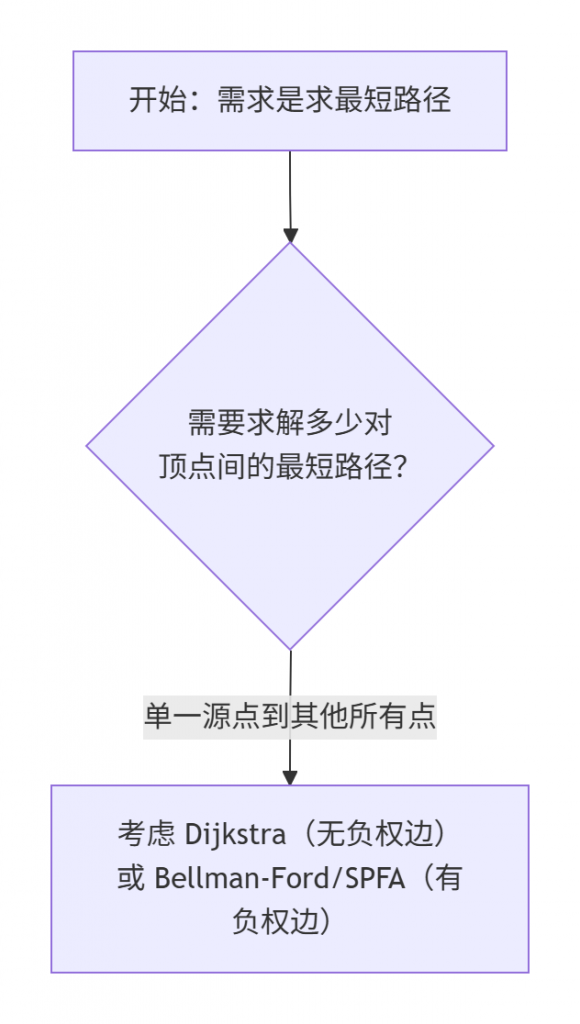
从上图可以看出,Floyd算法在以下一个或多个条件满足时,是非常合适的选择:
- 需求是所有顶点对之间的最短路径:这是Floyd的核心应用场景。
- 图中存在负权边:Floyd算法能够处理含有负权边的图(只要没有负权环),而Dijkstra算法在此情况下无法工作。
- 需要检测图中是否存在负权环:Floyd算法结束后,可以通过检查距离矩阵的主对角线元素是否出现负数来方便地检测负权环。
- 图规模不大或非常稠密:当顶点数不是特别多(例如几百个),或者图非常稠密(边数接近完全图)时,Floyd的常数小、实现简单的优势会更明显。对于稠密图,其效率可能高于执行|V|次Dijkstra算法。
反之,如果图中全是非负权边,且只需要求单源最短路径,那么Dijkstra算法(特别是堆优化版本)通常是更高效的选择。如果图的顶点规模非常大,那么O(∣V∣³)的时间复杂度将使Floyd算法难以承受。
