二叉堆 – 红栗

二叉堆是一棵完全二叉树，树中每个结点的值都不小于（或不大于）其左右孩子结点的权值。
二叉堆是一种支持插入、删除、查询最值的数据结构。
二叉堆一般分为大顶堆（大根堆）和小顶堆（小根堆）：
大顶堆：每个节点的值都大于或等于其子节点的值，在堆排序算法中用于升序排列。
小顶堆：每个节点的值都小于或等于其子节点的值，在堆排序算法中用于降序排列。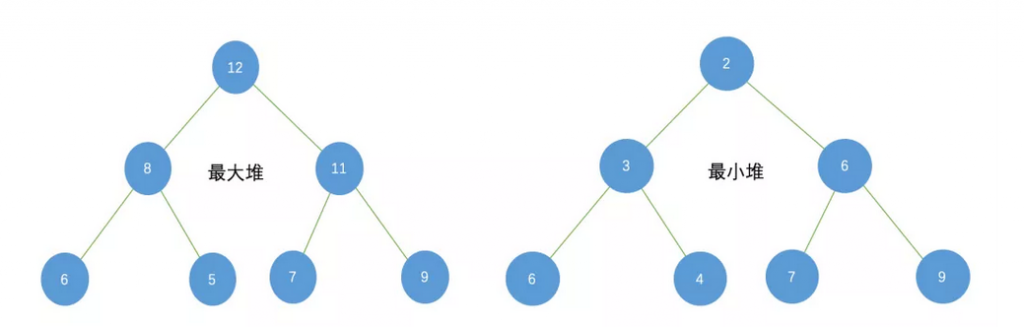大顶堆的根结点元素有最大值，小顶堆的根结点元素有最小值。下面都以小顶堆为例进行讲解。

堆可以看成一棵完全二叉树。用数组来保存的二叉堆，树中的每个结点与数组中存放的元素对应。树的每一层，除了最后一层可能不满，其他每一层都是满的。
二叉堆中的每个结点，都是以它为父结点的子树的最小值。下面是用数组实现的二叉堆。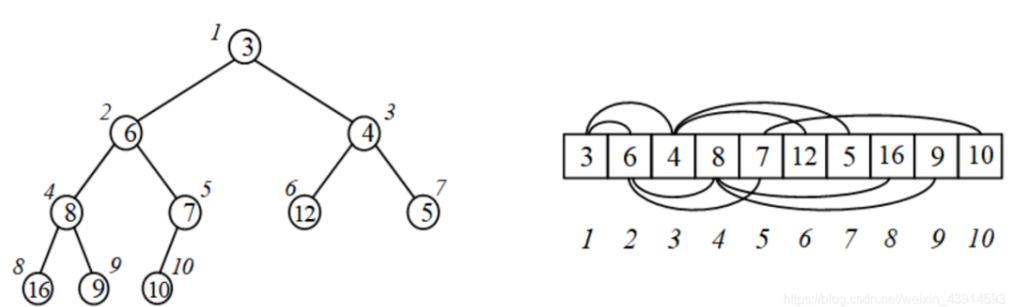

用数组A[]存储完全二叉树，结点数量为n，A[0]不用，A[1]为根结点，有以下性质：
- （1）i > 1的结点，其父结点位于i/2；
- （2）如果2i > n，那么i没有孩子；如果2i+1 > n，那么i没有右孩子；
- （3）如果结点i有孩子，那么它的左孩子是2i，右孩子是2i+1。
堆的操作有进堆和出堆。
- （1）进堆：每次把元素放进堆，都调整堆的形状，使得根结点保持最小。
- （2）出堆：每次取出的堆顶，就是整个堆的最小值；同时调整堆，使得新的堆顶最小。
- （3）获取堆顶，即A[1]。
复杂度：二叉树只有logn层，进堆和出堆逐层调整，都是O(logn)的。

二叉堆的实现 堆的具体实现有两个方法：上浮、下沉。
上浮：某个结点的优先级上升，或者在堆底加入一个新元素（建堆，把新元素加入堆），此时需要从下至上恢复堆的顺序。
下沉：某个结点的优先级下降，或者将根结点替换为一个较小的新元素（取出堆顶，用其他元素替换它），此时需要从上至下恢复堆的顺序。
新元素2进堆后，上浮: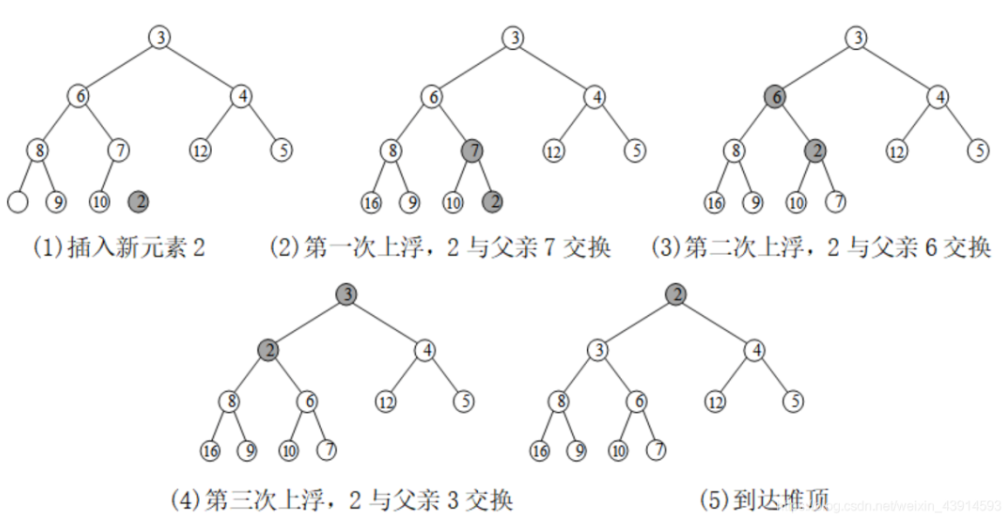
堆顶元素2出堆后，下沉: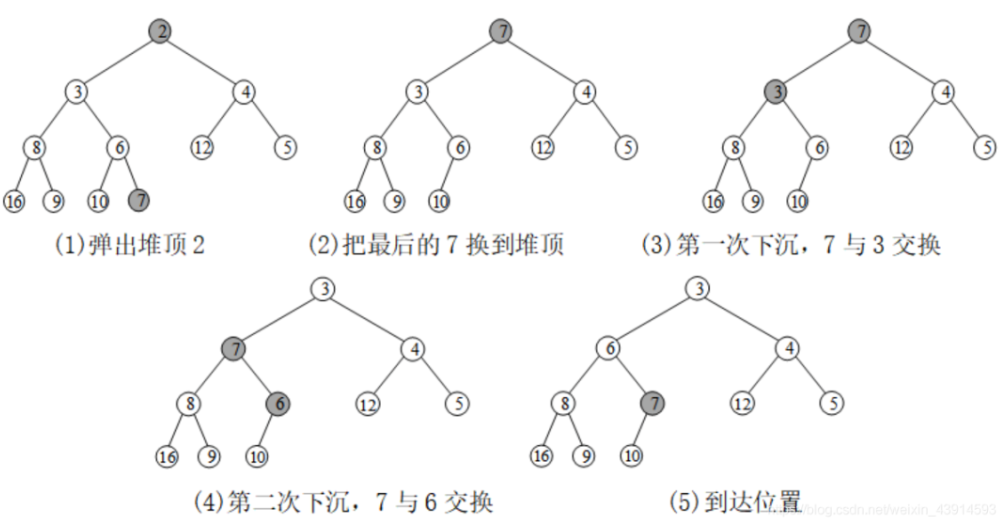堆经常用于实现优先队列，上浮对应优先队列的插入push()，下沉对应优先队列的删除队头pop()。

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。
（1）将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆，此堆为初始的无序区；
（2）将堆顶元素R[1]与最后一个元素R[n]交换，此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n]；
（3）由于交换后新的堆顶R[1]可能违反堆的性质，因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆，然后再次将R[1]与无序区最后一个元素交换，得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1，则整个排序过程完成。

#include<iostream>
using namespace std;
const int N=1e6+10;
int n,a[N],b[N],k=0; //k当前的堆的长度
void push(int x){ //插入数字 
    a[++k]=x;
    int i=k; 
    while(i>1&&a[i]<a[i/2]){ //小于父节点 
        swap(a[i],a[i/2]);
        i=i/2;
    }
} 
void pop(){ //删除最小数 
    a[1]=a[k];
    k--;
    int i=1;
    while(i<=k&&2*i<=k){ //存在左孩子 
        if(2*i+1<=k&&a[2*i+1]<a[2*i]&&a[2*i+1]<a[i]){//右孩子更小 
            swap(a[i],a[2*i+1]); 
            i=2*i+1; //继续处理右孩子
        }else if(a[2*i]<a[i]){ //只有左孩子更小 
            swap(a[i],a[2*i]); 
            i=2*i; //继续处理左孩子 
        }else{
            break; //如果不比孩子小 
        } 
    }
}
void heapsort(){ //堆排序：从小到大
    for(int i=1;i<=n;i++){
	b[i]=a[1]; //获取队首
	pop();//队首出队
    }
}
int main(){
    scanf("%d",&n); 
    for(int i=1;i<=n;i++){
    	int x;
        scanf("%d",&x); 
        push(x); //插入元素到优先队列 
    }
    heapsort(); 
    for(int i=1;i<=n;i++) printf("%d\n",b[i]);
    return 0;
}