排序

常见排序算法可以分为两大类：
比较类排序：通过比较来决定元素间的相对次序，由于其时间复杂度不能突破O(nlogn)，因此也称为非线性时间比较类排序。
非比较类排序：不通过比较来决定元素间的相对次序，它可以突破基于比较排序的时间下界，以线性时间运行，因此也称为线性时间非比较类排序。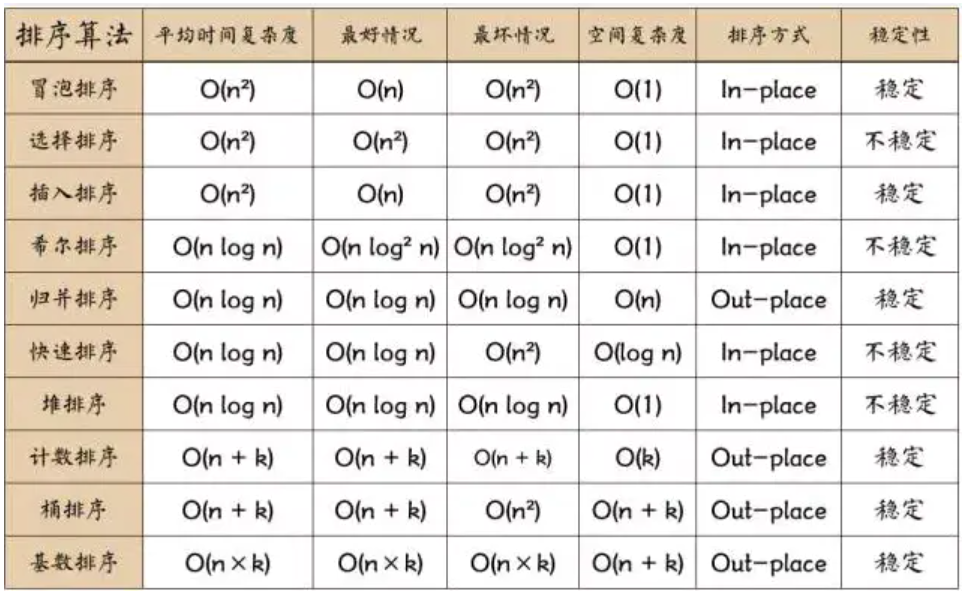 
稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面。排序前后相同元素的相对位置不变，则称排序算法是稳定的，否则排序算法是不稳定的。如原序列ri=rj且ri位于rj之前，排序后ri仍在rj之前，则称该排序是稳定的。
不稳定：如果a原本在b的前面，而a=b，排序之后 a 可能会出现在 b 的后面。

一、冒泡排序
1、比较相邻的元素。如果第一个比第二个大，就交换它们两个；
2、对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样在最后的元素应该会是最大的数；
3、针对所有的元素重复以上的步骤，除了最后一个；
4、重复步骤1~3，直到排序完成。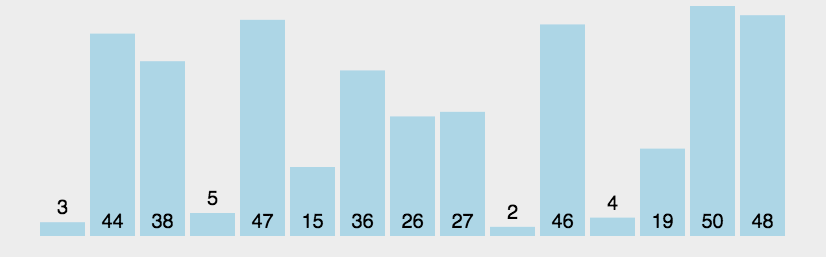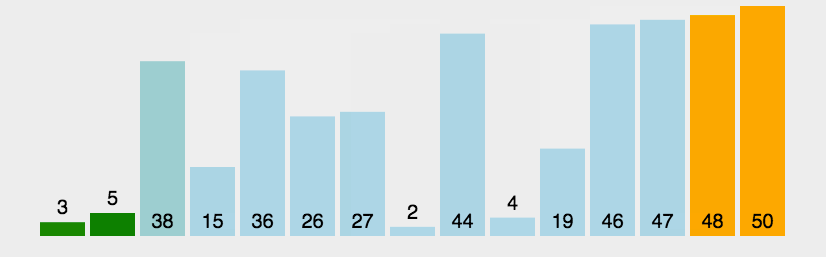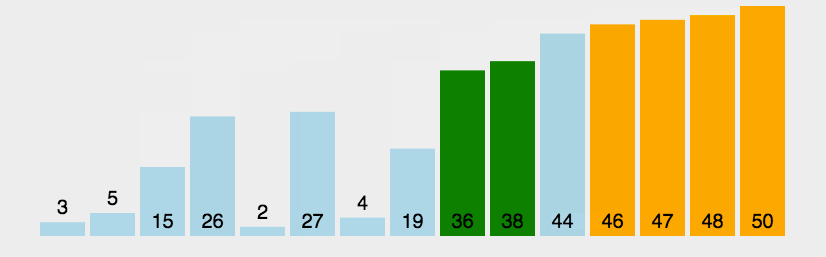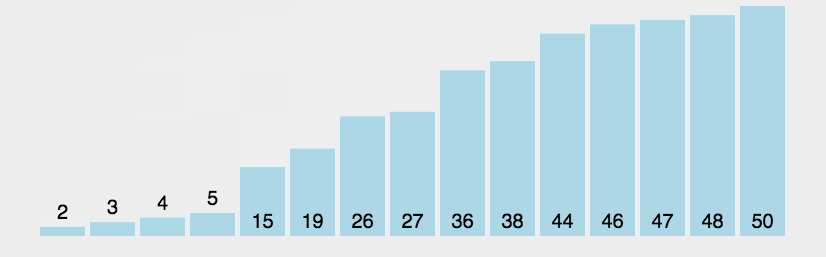

#include<iostream>
using namespace std;
int a[10010],n; 
int main(){
    cin>>n;  //元素n个
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1; i<=n-1; i++) {   //比较n-1轮
        for(int j=1;j<=n-1;j++) {  //每一轮比较n-1次
            if(a[j]>a[j+1]){  // 相邻元素两两对比
                int temp=a[j+1]; // 元素交换
                a[j+1]=a[j];
                a[j]=temp;
            }
        }
    }
    for(int i=1;i<=n;i++) cout<<a[i]<<' ';
    return 0;
}

改进的思路：如果第i轮循环结束，没有产生过任何交换，说明第i轮结束后，数组有序, 则不需要下一轮循环。这个思路，请学员自行设计代码完成。

二、选择排序 首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。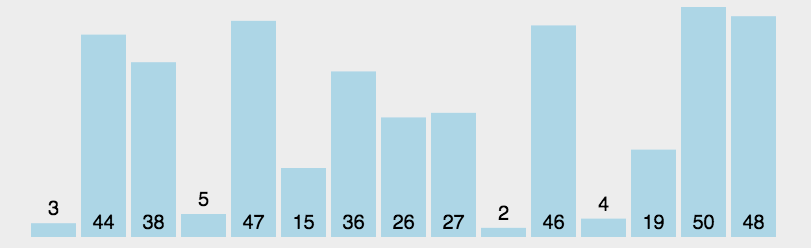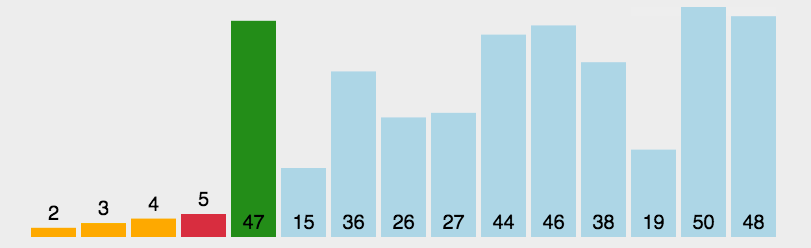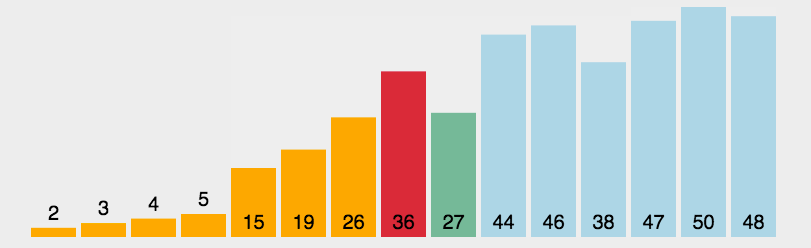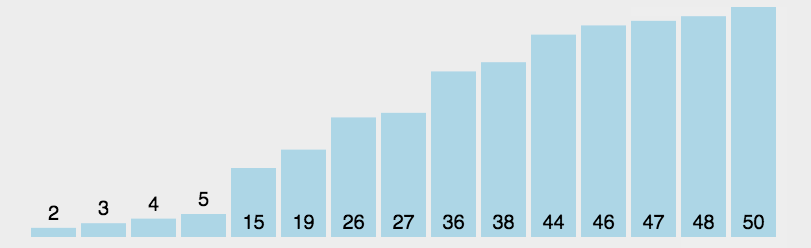 

#include<iostream>
using namespace std;
int a[10010],n; 
int main(){
    cin>>n;  //元素个数为n个
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<=n-1;i++){
        int mi=i;//最小数的下标，初始值是第i项
        for(int j=i+1;j<=n;j++){
            if(a[j]<a[mi]){  //寻找到一个新的最小的数
                mi=j;        //将最小数的下标更新
            }
        }
        int temp=a[i];   //完成最小数与第i个数交换
        a[i]=a[mi];
        a[mi]=temp;
    }
    for(int i=1;i<=n;i++) cout<<a[i]<<' ';
    return 0;
}

无论什么数据进去都是O(n²)的时间复杂度。在与最小数交换时，有可能使得不应该排到后面的数字被交换到后面去。

三、插入排序 插入排序将数组分成前后2块，前一块：有序区间；后一块：无序区间；
排序思想：从无序区间中选择一个数字，插入到有序区间中。
有序区间扩大一位，无序区间减少一位。直到有序区间覆盖整个数组。
无序区间：i到n-1；有序区间：0到i-1。
插入的关键：我们需要找到有序区间中插入的位置j后面，然后将有序区间j后面的数字往后移动一位，将j的位置腾出来，放置需要插入的数字。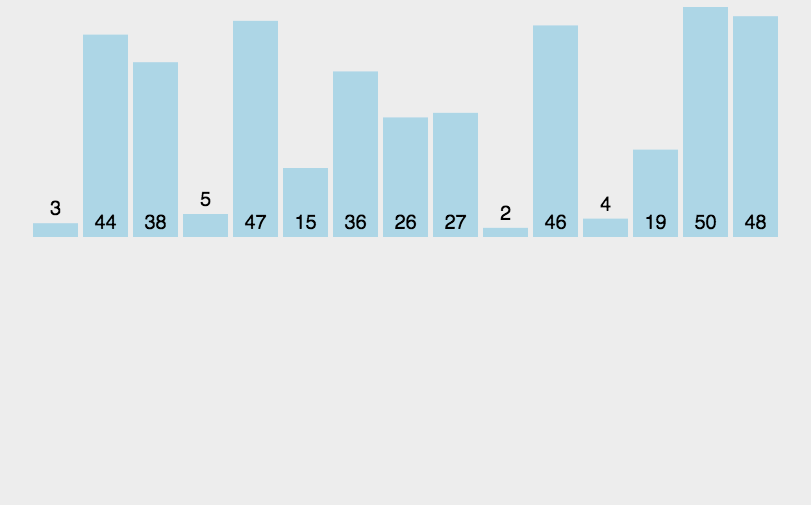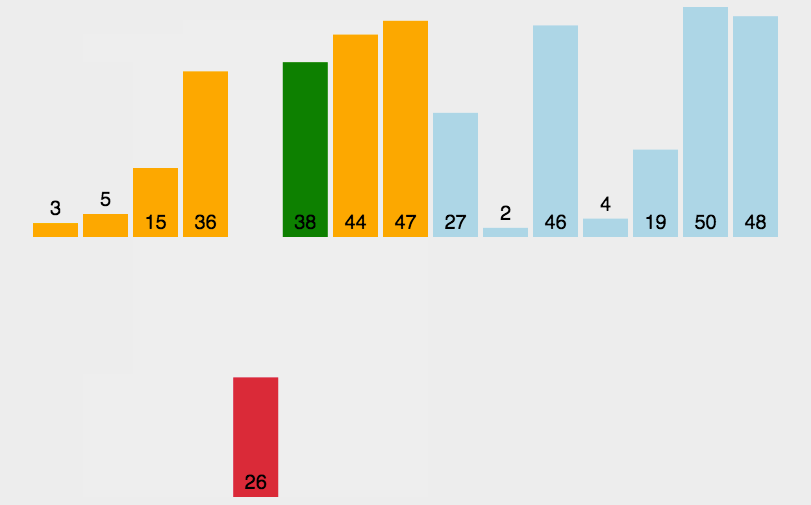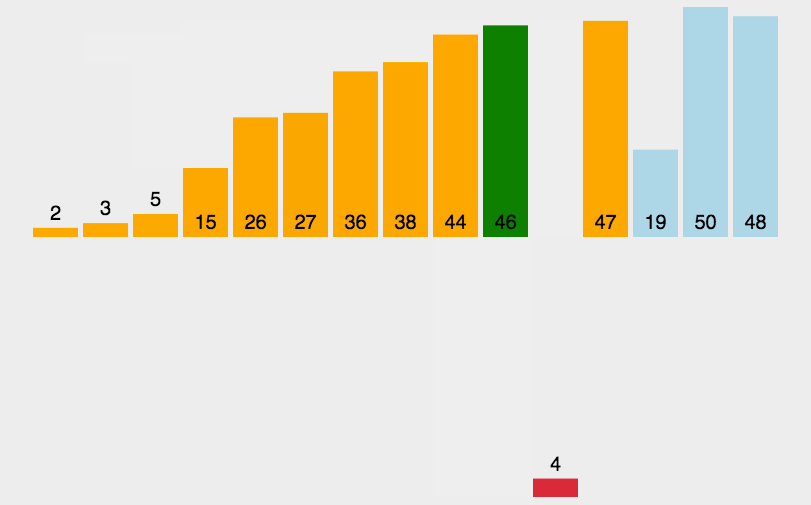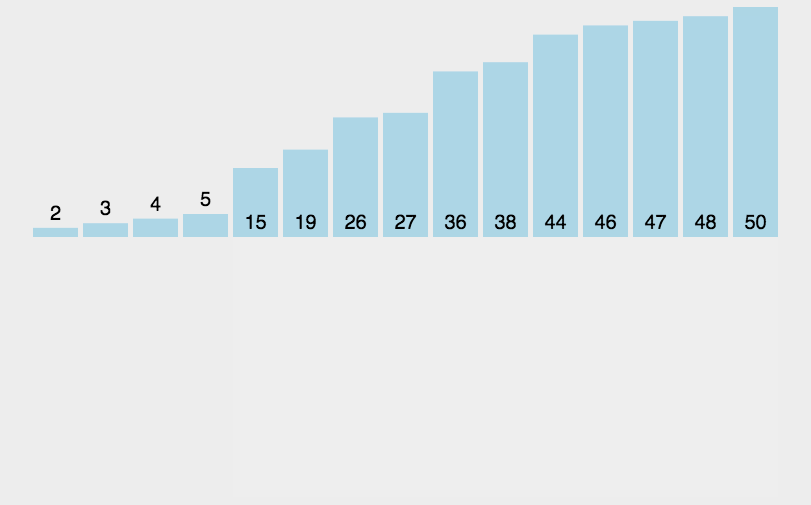

#include<iostream>
using namespace std;
int a[10010],n; 
int main(){
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=2;i<=n;i++){
        int pi=i-1;
        int vi=a[i]; //第i个位置的元素
        while(pi>=1&&a[pi]>vi){//与前面比,小于前面的,则前面的往后移
            a[pi+1]=a[pi];  
            pi--;//继续往前比
        }
        a[pi+1]=vi;//移到不能移，最后一个比较位置更新为第i个位置的元素
    }
    for(int i=1;i<=n;i++) cout<<a[i]<<' ';
    return 0;
}

四、桶排序

桶排序也叫箱排序。工作原理是：统计每个元素出现的次数，然后利用桶的下标已经有序的原理，按照每个数出现的次数循环输出，因此，桶排序要求数组元素数值必须是小范围内的数！

for(int i=1;i<=n;i++){ //假设输入n个数字
    cin>>x;
    a[x]++; //统计x出现的次数
    maxNum=max(a[x],maxNum);
}
for(int i=0;i<=maxNum;i++){//maxNum是输入的最大数字
    while(a[i]--){
        cout<<i<<' '; //排序结果
    }
}

五、计数排序
计数排序的思想：1、计算每个数出现了几次；2、求出每个数出现次数的前缀和；3、利用出现次数的前缀和从右边至左计算每个数的排名。

for(int i=1;i<=n;i++){ //假设输入n个数字
    cin>>a[i];
    cnt[a[i]]++; //统计a[i]出现的次数
    maxNum=max(a[i],maxNum);
}
for(int i=1;i<=maxNum;i++){//maxNum是输入的最大数字
    cnt[i]=cnt[i-1]+cnt[i]; //出现次数的前缀和
}
for(int i=n;i>=1;i--){//逆序求出每个数正确的排序位置
    b[cnt[a[i]]--]=a[i]; //逆序是为了保证稳定性
}
for(int i=1;i<=n;i++) cout<<b[i]<<' ';//排序结果

六、快速排序
选择一个参考值，将数组一分为二，使得数组的左侧都<=mid，数组的右侧都>=mid；然后继续对每个区间重复上述步骤，直到整个数组有序。

void qsort(int a[],int l,int r){
    if(l>=r) return;
    int mid=a[(l+r)/2],i=l,j=r;//mid是参考值选取
    while(i<=j){
        while(a[i]<mid) i++;
        while(a[j]>mid) j--;
        if(i<=j){
            swap(a[i],a[j]);
            i++;j--;
        }
    }
    qsort(l,j);
    qsort(i,r);
}

快排可以直接调用<algorithm>中的sort()函数。
sort(begin(), end(), cmp);
begin()待排序数组的首地址
end() 是待排序数组的尾地址的下一个
cmp 是排序规则，默认是升序

七、归并排序

void msort(int a[],int b[],int l,int r){
    if(l>=r)return;
    int mid=(l+r)/2,i=l,j=mid+1,k=l;//将数组一分为二
    msort(l,mid);
    msort(mid+1,r);
    while(i<=mid&&j<=r){ //合并左、右区间
        if(a[i]<=a[j]) b[k++]=a[i++];
        else b[k++]=a[j++];
    }
    while(i<=mid)b[k]=a[i],k++,i++;
    while(j<=r)b[k]=a[j],k++,j++;
    for(int i=l;i<=r;i++)a[i]=b[i];
}

八、堆排序
堆排序是指利用堆这种数据结构所设计的一种排序算法。
（1）将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆，此堆为初始的无序区；
（2）将堆顶元素R[1]与最后一个元素R[n]交换，此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n]；
（3）由于交换后新的堆顶R[1]可能违反堆的性质，因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆，然后再次将R[1]与无序区最后一个元素交换，得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1，则整个排序过程完成。

#include<iostream>
using namespace std;
const int N=1e6+10;
int n,a[N],b[N],k=0; //k当前的堆的长度
void push(int x){ //插入数字 
    a[++k]=x;
    int i=k; 
    while(i>1&&a[i]<a[i/2]){ //小于父节点 
        swap(a[i],a[i/2]);
        i=i/2;
    }
} 
void pop(){ //删除最小数 
    a[1]=a[k];
    k--;
    int i=1;
    while(i<=k&&2*i<=k){ //存在左孩子 
        if(2*i+1<=k&&a[2*i+1]<a[2*i]&&a[2*i+1]<a[i]){//右孩子更小 
            swap(a[i],a[2*i+1]); 
            i=2*i+1; //继续处理右孩子
        }else if(a[2*i]<a[i]){ //只有左孩子更小 
            swap(a[i],a[2*i]); 
            i=2*i; //继续处理左孩子 
        }else{
            break; //如果不比孩子小 
        } 
    }
}
void heapsort(){ //堆排序：从小到大
    for(int i=1;i<=n;i++){
	b[i]=a[1]; //获取队首
	pop();//队首出队
    }
}
int main(){
    scanf("%d",&n); 
    for(int i=1;i<=n;i++){
    	int x;
        scanf("%d",&x); 
        push(x); //插入元素到优先队列 
    }
    heapsort(); 
    for(int i=1;i<=n;i++) printf("%d\n",b[i]);
    return 0;
}

九、基数排序 基数代表一个数的进制数，例如计算机采用的是二进制系统，它的特点是逢2进1，这个2就是基数。10进制的计数是10,8进制的基础是8。
按照从低位到高位的顺序，比较多位数的每一位来排序的。排序的过程中，需要准备基数个“桶”，所以叫做基数排序。以十进制为例，基数排序的过程如下：
（1）将所有需要排序的整数的位数统一，数位较短的高位补零（不用真的补）。
（2）根据最低位（个位）排列数字，进桶。
（3）根据下一个位置（十位）排列数字，如果这个位置上的数值相同，那么数字之间的顺序根据上一轮的排序确定。（本质上，就是把上一轮的排序结果写回数组；然后再次按照十位进桶，写回；按照百位进桶、写回；以此类推… 。桶用数列实现即可）
（4）直到按照最高位进桶、写回完成，此时数列就变成一个有序序列。

#include<iostream>
#include<queue>
using namespace std;
int n,a[100010],k=0; //w表示数位，1是个位，10是十位...
queue<int> q[10];
int main(){
    cin>>n;
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);
    //w表示数位，1是个位，10是十位，100是百位... 
    for(int w=1;w<=1e9;w*=10){//w最多到题目数据位数范围
        for(int i=1;i<=n;i++) q[a[i]/w%10].push(a[i]); 
        k=0;
        for(int i=0;i<=9;i++)
            while(q[i].size()){
                a[++k]=q[i].front();
                q[i].pop();
            }
    }
     
    for(int i=1;i<=n;i++) printf("%d\n",a[i]);
    return 0;
}