质数筛法

• 约数
  • 对于两个整数 a，b 存在两个整数 q, r 满足 b = aq + r (0 <= r <= |a|)。
  • 当 r = 0 时 我们称 a 整除 b，即 a | b。
  • 对于两个正整数 a, b，如果有 a | b，那么称 a 是 b 的约数。
• 合数 除了 1 和他本身还有其他约数 (>0) 的数是合数. 4 是最小合数。
• 质数 称一个数为质数当且仅当这个数的质因子只有 1 和他本身。
  • 「1 不是质数」
  • 「2是最小的质数,也是唯一一个同时是偶数也是质数的数.」

一、质数的判断：试除法

bool isPrime(int k) {
    if(k < 2)  //k小于2，不是质数
      return false;

   for(int i=2; i<=k/i; i++){  //i<=k/i 相当于 i<=sqrt(k);
      if(k%i==0){  //找到因子，不是质数
          return false;
      }
  }
   return true;
}

高效方法 首先看一个关于质数分布的规律：大于等于5的质数一定和 6 的倍数相邻。例如5和7，11和13, 17和19等等；
证明：
令x≥1，将大于等于5的自然数表示如下：
······ 6x-1，6x，6x+1，6x+2，6x+3，6x+4，6x+5，6(x+1），6(x+1)+1 ······
可以看到，不在6的倍数两侧，即6x两侧的数为6x+2，6x+3，6x+4，由于2(3x+1)，3(2x+1)，2(3x+2)，所以它们一定不是素数，再除去6x本身.
显然，素数要出现只可能出现在 6x 的相邻两侧。
在6的倍数相邻两侧并不是一定就是质数。
此时判断质数以6为单元快进，即将循环中i++步长加大为6，加快判断速度，原因是，假如要判定的数为 n，则 n 必定是 6x-1 或 6x+1 的形式，对于循环中 6i-1，6i，6i+1, 6i+2，6i+3，6i+4，其中如果 n 能被 6i，6i+2，6i+4 整除，则 n 至少得是一个偶数，但是 6x-1 或 6x+1 的形式明显是一个奇数，故不成立；另外，如果 n 能被6i+3 整除，则 n 至少能被 3 整除，但是 6x 能被3整除，故 6x-1 或 6x+1（即n）不可能被3整除，故不成立。综上，循环中只需要考虑 6i-1 和 6i+1 的情况，即循环的步长可以定为 6，每次判断循环变量 k 和 k+2 的情况即可，理论上讲整体速度应该会是上面方法的3倍。

bool isPrime(int n) {
    if(n==2||n==3)
      return true;
   if(n%6!=1&&n%6!=5)
     return false;

 int tmp=sqrt(n);
 for(int i=5;i<=tmp;i+=6)
     if(n%i==0||n%(i+2)==0)
       return false;
 return true;
}

二、质数筛法
显然, 在所有大于 0 的自然数中, 除了质数就是合数。要求质数, 只需要 “筛” 去所有的合数即可。筛去合数要比依次判断每个数是否时质数要快的多。
练习 给定一个范围 n，有 q 个询问，每次输出第 k 小的素数。（n = 10⁸，1≤ q ≤ 10⁶，保证查询的素数不大于 n。）

朴素筛法 – 埃氏筛法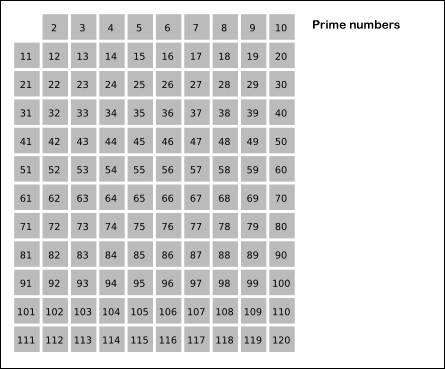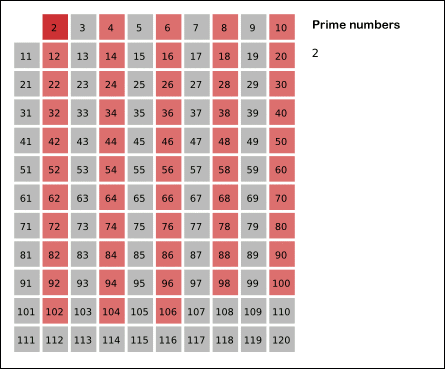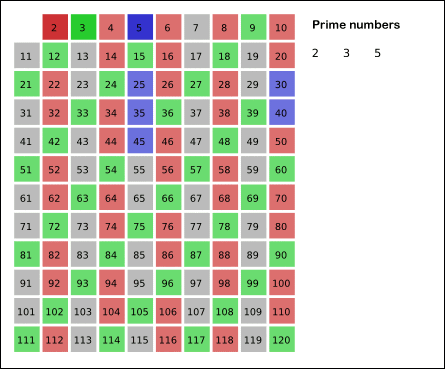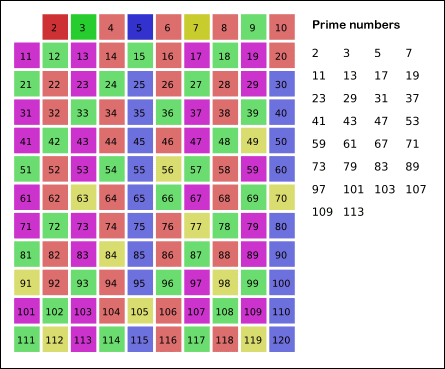一个素数 p 只有 1 和 p 这两个约数，并且它的约数一定不大于其本身。因此，我们下边方法来筛选出来素数：
1、把从2开始的、某一范围内的正整数从小到大顺序排列；
2、剩下的数中选择最小的素数，然后去掉它的倍数。
3、依次类推，直到循环结束。

#include <cstdio>
using namespace std;
const int N=1e8+8;
int p[N],cnt=0;
bool st[N];  //值为0是质数，为1是合数
int n,q;
void get_primes(int n){ //质数筛
  for(int i=2;i<=n;i++){
     if(st[i])
       continue;
 
     p[++cnt] = i;
     for(int j=i+i;j<=n;j+=i){
          st[j] = 1;
     }
   }
}
 
int main(){
    scanf("%d %d",&n,&q);
    get_primes(n);
 
    int x;
    while(q--){
      scanf("%d", &x);
      printf("%d\n", p[x]);
    }
    return  0;
}

线性筛-欧拉筛 欧拉筛法的基本思想 ：在埃氏筛法的基础上，让每个合数只被它的最小质因子筛选一次，以达到不重复的目的。参考代码：

#include<cstdio>
using namespace std;
const int N=1e8+8;
int p[N],cnt=0;
bool st[N];
int n,q;

void get_primes(int n){
    for(int i=2;i<=n;i++){
        if(st[i]==0)
            p[++cnt]=i;

    for(int j=1;i*p[j]<=n;j++){
        st[i*p[j]]=1; //标记
        if(i%p[j]==0) //核心操作,保证了O(n)的复杂度
            break;
        }
    }
}

int main(){
    scanf("%d %d",&n,&q);
    get_primes(n);

    int x;
    while(q--){
        scanf("%d",&x);
        printf("%d\n",p[x]);
    }
    return 0;
}

解析 算术基本定理——任何一个大于1的自然数 N,如果 N 不为质数,那么 N 可以唯一分解成有限个质数的乘积。如何筛去合数, 这里就应用到了算术基本定理. 关于合数,这里我们需要注意两点:

• 所有合数都要筛到
• 不能有重复筛选, 否则无法达到在线性时间内的运行了

要做到第一点,根据算术基本定理: n = q * m (q表示最小质数, m = n/q,显然 m >= q), 对N内的m和q进行枚举

for(某个数m; m <= N; m++){ for(小于或等于 m 的质数q; q*m <= N;){…} }

这样我们就保证了能枚举 N 以内的所有整数, 然而我们还不能保证枚举的合数不重复。

先来思考一下为什么会有重复, 由于对于任意一个 n=m*q , m 和 q 是相对的两个状态, m 大了q 就变小, m 小了 q 就变大。设 n = m1 * q1 = m2 * q2,  q1 <= q2 <= m2 <= m1 我们这里需要保证当且仅当在 q1是最小质因数时能求解, 也就是去除 q2 和 m2 的情况.因为 q1 与 q2 互质, 且 q1<q2 , 则有 m2 % q1 = 0;

所以关键步骤来了: if(i % p[j]==0) break;

当 i 是 p[j] 的倍数时直接跳出循环.

设 i = p[j] * t 此时有 i * p[j+1] = p[j] * t * p[j+1]

可以看到此时的最小质数时 p[j], 为了避免与当 m = p[j+1] * t 时有重复,这里可以通过break跳过计算

此外还需注意: 要保证 m 从 2 开始, 因为 1 * q = 1 且 i%1==0;

举个例子：

i = 8 ，j = 1，prime[j] = 2，如果不跳出循环，p[j+1] = 3，8 * 3 = 2 * 4 * 3 = 2 * 12，在 i = 12 时会计算。因为欧拉筛法的原理便是通过最小素因子来消除。

小结：埃筛是筛去每个质数的倍数；欧筛是筛去每个自然数的质数倍。