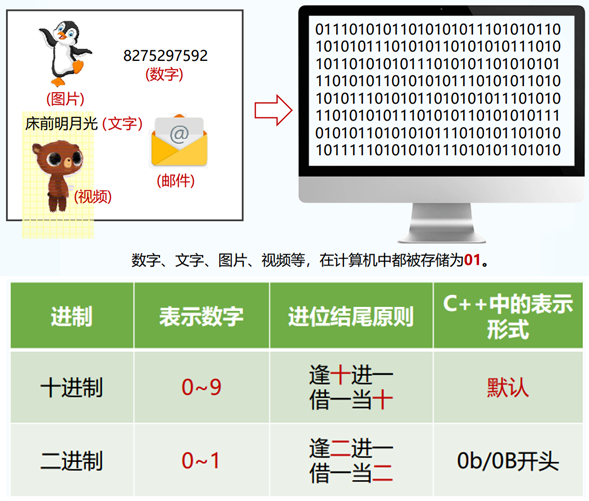
所有计算机都是电子设备,可以做一件事:检测电信号是“打开”还是“关闭”。因此,早期的计算机科学家认识到,用只有数字 0 和 1(基数为2) 的二进制系统,比我们生活中常用的十进制数系统对操作计算机更为便捷。
数码:数制中表示基本数值大小的不同数字符号。例如,十进制有10个数码:0、1、2、3、4、5、6、7、8、9;而二进制只有2个数码:0和1。
基数:数制所使用数码的个数。例如,二进制的基数为2;十进制的基数为10。
位权:数制中某一位上的1所表示数值的大小(所处位置的价值)。例如,十进制的123,1的位权是100,2的位权是10,3的位权是1。二进制中的 1011 (一般从左向右开始),第一个1的位权是8,0的位权是4,第二个1的位权是2,第三个1的位权是1。
计数:计数的规则。在人们使用最多的进位计数制中,表示数的符号在不同的位置上时所代表的数的值是不同的。
 十进制:人们在日常生活中最熟悉的进位计数制。在十进制中,数用0,1,2,3,4,5,6,7,8,9这十个符号来描述。计数规则是逢十进一。
十进制:人们在日常生活中最熟悉的进位计数制。在十进制中,数用0,1,2,3,4,5,6,7,8,9这十个符号来描述。计数规则是逢十进一。
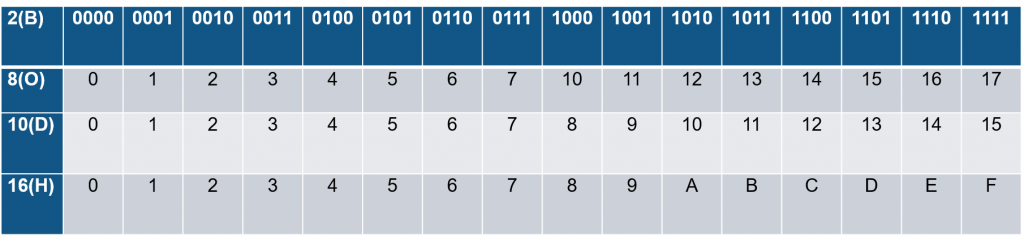
二进制:在计算机系统中采用的进位计数制。在二进制中,数用0和1两个符号来描述。计数规则是逢二进一,借一当二。
八进制:每一位可取0~7这8个数码,计数的基数为8,超过7须用多位数来表示。
十六进制:人们在计算机指令代码和数据的书写中经常使用的数制。在十六进制中,数用0,1,…,9和A,B,…,F(或a,b,…,f)16个符号来描述。计数的基数为16,超过F须用多位数来表示。
#include <bits/stdc++.h>
using namespace std;
int main(){
int a = 10;
cout<<a<<endl;
int b = 010;//0开头表示8进制
cout<<b<<endl;//将8进制的10转换为10进制打印
int c = 0x10;//0x开头代表16进制
cout<<c<<endl;//将16进制的10转换为10进制打印
double d=1e2;//科学计数,1 * 10的平方
cout<<d<<endl;
double e=1e-2;//科学计数,1 * 10的-2次方
cout<<e<<endl;
return 0;
} 二进制转十进制:按位权展开后求和 小数部分的位权从左往右依次是-1,-2,-3… …
二进制转十进制:按位权展开后求和 小数部分的位权从左往右依次是-1,-2,-3… …
例:(1011.01)2=(1×23 + 0×22 + 1×21 + 1×20 + 0×2-1 + 1×2-2)10=(8+0+2+1+0+0.25)10=(11.25)10
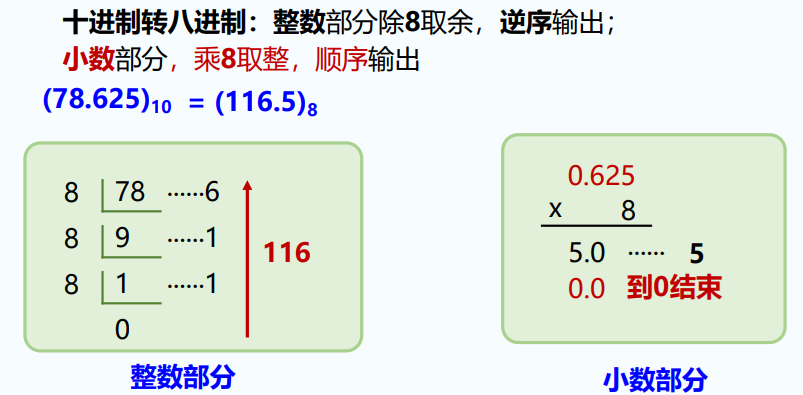
十进制转二进制:
整数转换: 十进制整数转换为K进制整数的方法是倒除法,即除K直到商为0,倒取余数。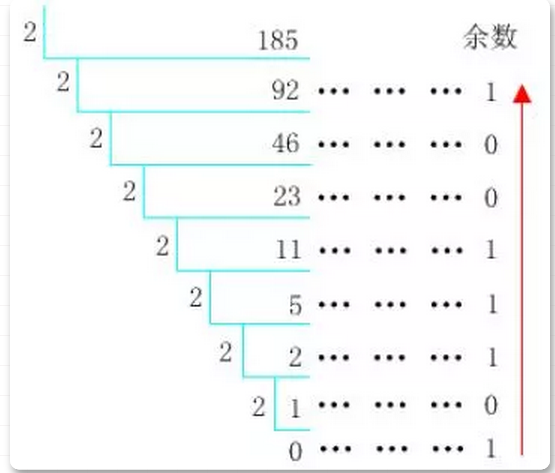 所以 (185)10=(10111001)2
所以 (185)10=(10111001)2
小数部分转换: 十进制小数转换为K进制小数的方法是乘2取整法,即小数部分循环乘以K直至为0,顺序取整数部分。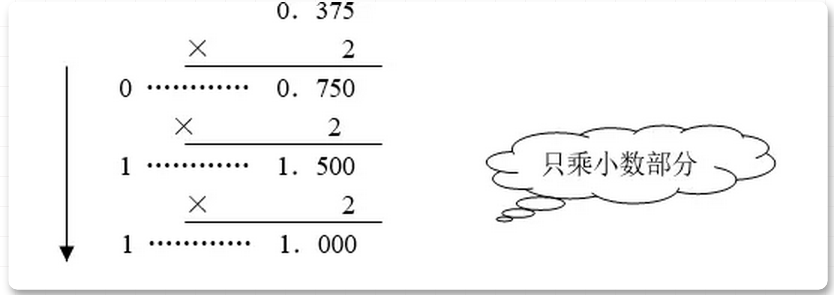 (0.375)10=(0.011)2
(0.375)10=(0.011)2
八进制与二进制的转换 (8421法)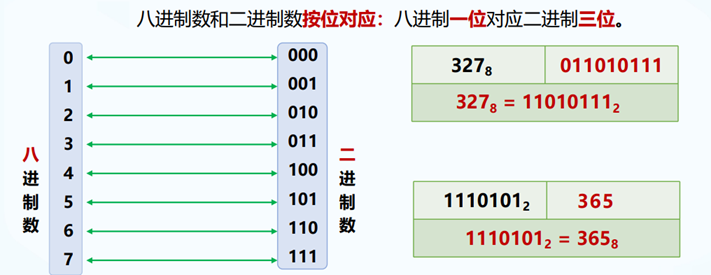
例:将八进制的37.416转换成二进制数:一位转三位 。即:(37.416)10=(11111.10000111)2
例:将二进制的10110.0011 转换成八进制:三位转一位。即:(10110.011)2=(26.14)10
十六进制与二进制的转换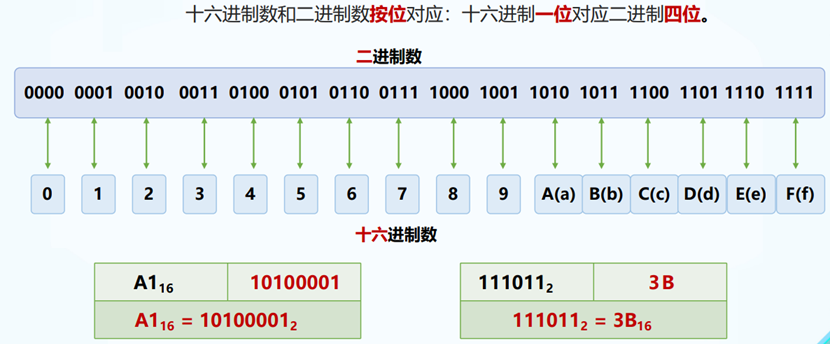
例:将十六进制数5DF.9 转换成二进制:一位转四位 即:(5DF.9)16=(10111011111.1001)2
例:将二进制数1100001.111 转换成十六进制:四位转一位 即:(1100001.111)2=(61.E)16
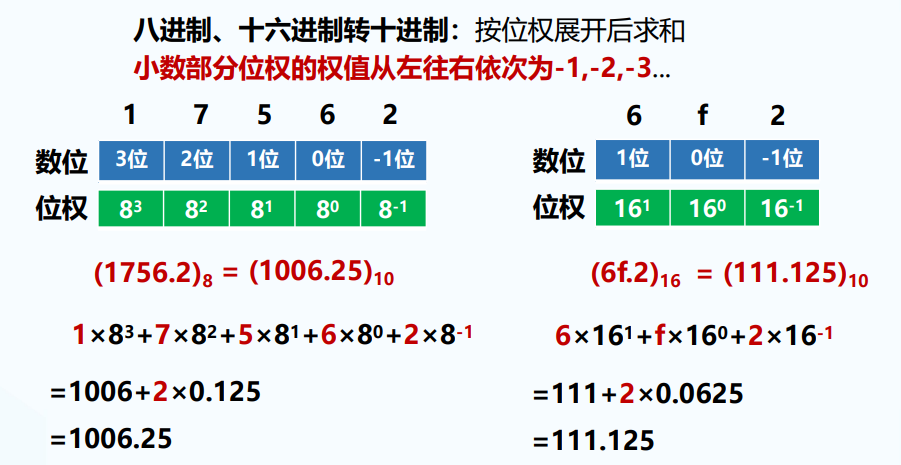
八进制、十六进制转十进制:按位权展开后求和