一、递归的定义
在数学与计算机科学中,递归(Recursion)是指在函数的定义中使用函数自身的方法。
实际上,递归,顾名思义,其包含了两个意思:递 和 归,这正是递归思想的精华所在。
二、递归思想的内涵(递归的精髓是什么?)
正如上面所描述的场景,递归就是有去(递去)有回(归来)。“有去”是指:递归问题必须可以分解为若干个规模较小,与原问题形式相同的子问题,这些子问题可以用相同的解题思路来解决;“有回”是指 : 这些问题的演化过程是一个从大到小,由近及远的过程,并且会有一个明确的终点(临界点),一旦到达了这个临界点,就不用再往更小、更远的地方走下去。最后,从这个临界点开始,原路返回到原点,原问题解决。
更直接地说,递归的基本思想就是把规模大的问题转化为规模小的相似的子问题来解决。
特别地,在函数实现时,因为解决大问题的方法和解决小问题的方法往往是同一个方法,所以就产生了函数调用它自身的情况,这也正是递归的定义所在。格外重要的是,这个解决问题的函数必须有明确的结束条件,否则就会导致无限递归的情况。
三、递归的三要素
1). 明确递归终止条件
我们知道,递归就是有去有回,既然这样,那么必然应该有一个明确的临界点,程序一旦到达了这个临界点,就不用继续往下递去而是开始实实在在的归来。换句话说,该临界点就是一种简单情境,可以防止无限递归。
2). 给出递归终止时的处理办法
我们刚刚说到,在递归的临界点存在一种简单情境,在这种简单情境下,我们应该直接给出问题的解决方案。一般地,在这种情境下,问题的解决方案是直观的、容易的。
3). 提取重复的逻辑,缩小问题规模
我们在阐述递归思想内涵时谈到,递归问题必须可以分解为若干个规模较小、与原问题形式相同的子问题,这些子问题可以用相同的解题思路来解决。从程序实现的角度而言,我们需要抽象出一个干净利落的重复的逻辑,以便使用相同的方式解决子问题。
四、递归算法的编程模型
在我们明确递归算法设计三要素后,接下来就需要着手开始编写具体的算法了。在编写算法时,不失一般性,我们给出两种典型的递归算法设计模型,如下所示。
模型一: 在递去的过程中解决问题
function recursion(大规模){
if (end_condition){ // 明确的递归终止条件
end; // 简单情景
}else{ // 在将问题转换为子问题的每一步,解决该步中剩余部分的问题
solve; // 递去
recursion(小规模); // 递到最深处后,不断地归来
}
}
模型二: 在归来的过程中解决问题
function recursion(大规模){
if (end_condition){ // 明确的递归终止条件
end; // 简单情景
}else{ //先将问题全部描述展开,再由尽头“返回”依次解决每步中剩余部分的问题
recursion(小规模); // 递去
solve; // 归来
}
}五、递归的应用场景 递归算法一般用于解决三类问题:
(1). 问题的定义是按递归定义的(Fibonacci函数,阶乘,…);
(2). 问题的解法是递归的(有些问题只能使用递归方法来解决,例如,汉诺塔问题,…);
(3). 数据结构是递归的(链表、树等的操作,包括树的遍历,树的深度,…)。
在下文我们将给出递归算法的一些经典应用案例,这些案例基本都属于第三种类型问题的范畴。
举例:求裴波那契数列的第n项。
int num(int n){
if(n<=1) return n;
return num(n-1)+num(n-2);
}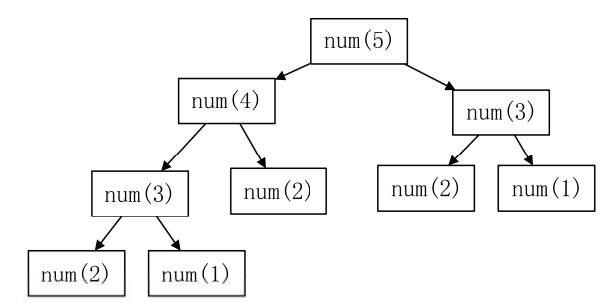
注意:当n越来越大时,这棵“树”会越来越大,重复求解的项数越来越多,非常耗时。从上面的结构来看,n每增加1,树就增加一层,从上往下的项数以2的指数级增加。
六、递归与循环
递归与循环是两种不同的解决问题的典型思路。
递归通常很直白地描述了一个问题的求解过程,因此也是最容易被想到解决方式。
循环其实和递归具有相同的特性,即做重复任务,但有时使用循环的算法并不会那么清晰地描述解决问题步骤。
单从算法设计上看,递归和循环并无优劣之别。然而,在实际开发中,因为函数调用的开销,递归常常会带来性能问题,特别是在求解规模不确定的情况下;而循环因为没有函数调用开销,所以效率会比递归高。递归求解方式和循环求解方式往往可以互换,也就是说,如果用到递归的地方可以很方便使用循环替换,而不影响程序的阅读,那么替换成循环往往是好的。
问题的递归实现转换成非递归实现一般需要两步工作:
(1). 自己建立“堆栈(一些局部变量)”来保存这些内容以便代替系统栈,比如树的三种非递归遍历方式;
(2). 把对递归的调用转变为对循环处理。
七、递归的缺点 递归算法解题的运行效率较低。在递归调用的过程当中系统为每一层的返回点、局部量等开辟了栈来存储。递归次数过多容易造成栈溢出等。常用的改进方法:递归改递推、带备忘录的递归。

八、几种常见的枚举形式和遍历方式:
| 枚举形式 | 状态空间规模 | 一般遍历方式 |
| 多项式 | nk, k为常数 | 循环(for)、递推 |
| 指数 | kn, k为常数 | 递归、位运算 |
| 排列 | n! | 递归、next_permutation |
| 组合 | \(C_{n}^{m}\) | 递归+剪枝 |
九、递归的机器实现
递归在计算机中是如何实现的 ? 换句话说,它最终被编译成什么样的机器语言 ? 这就要从函数调用说起。实际上,一台典型的32位计算机采用 “堆栈结构” 来实现函数调用,它在汇编语言中,把函数所需的第k个,第k – 1个,..第1个参数依次入栈,然后执行call(address)指令。该指令把返回地址(当前语句的下一条语句的地址)入栈,然后跳转到address位置的语句。在函数返回时,它执行ret指令。该指令把返回地址出栈,并跳转到该地址继续执行。
对于函数中定义的C + 局部变量,在每次执行call与ret指令时,也会在“栈”中相应地保存与复原,而作用范围超过该函数的变量,以及通过new和malloc函数动态分配的空间则保存在另一块称为 “堆”(注意, 这个堆与我们所说的二叉堆是两个不同的概念)的结构中。栈指针、 返回值、局部的运算会借助CPU的 “完成。由此我们可以得知:寄存器”
1. 局部变量在每层递归中都占有 – 份空间, 声明过多由此我们可以得知 : 或递归过深就会超过“栈”所能存储的范围,造成栈溢出。
2. 非局部变量对于各层连归都共享同份空间,需要及时维护、还原现场,以防止在各层递归之间存储和读取的数据互相影响。
了解了递归的机器实现之后,我们就可以使用模拟的方法,把递归程序改写为非递归程序。具体来说,我们可以使用一个数组来模拟栈,使用变量来模拟栈指针和返回值,使用 switch/case 或者goto/label 来模拟语句跳转。
