强联通分量

在有向图G中，如果两个顶点u，ｖ间有一条从ｕ到ｖ的有向路径，同时还有一条从ｖ到ｕ的有向路径，则称两个顶点强连通。如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向非强连通图的极大强连通子图，称为强连通分量。

强连通分量（Strongly Connected Components，SCC）的定义是：极大的强连通子图。

上图中有三个强连通分量，分别是a、b、e以及f、g和c、d、h

作用

通过 “缩点” 将有向图转为有向无环图 DAG (拓扑图).

Kosaraju算法

显然上图中有两个强连通分量，即强连通分量A和强连通分量B，分别由顶点A0-A1-A2和顶点B3-B4-B5构成。每个连通分量中有若干个可以相互访问的顶点（这里都是3个），强连通分量与强连通分量之间不会形成环，否则应该将这些连通分量看成一个整体，即看成同一个强连通分量。

我们假设，DFS从强连通分量B的任意一个顶点开始，那么恰好遍历整个图需要2次DFS，和连通分量的数量相等，而且每次DFS遍历的顶点恰好属于同一个连通分量。但是，我们若从连通分量A中任意一个顶点开始DFS，就不能得到正确的结果，因为此时我们只需要一次DFS就访问了所有的顶点。所以，我们不应该按照顶点编号的自然顺序（0,1,2，……）或者任意其它顺序进行DFS，而是应该按照被指向的强连通分量的顶点排在前面的顺序进行DFS。上图中由强连通分量A指向了强连通分量B。所以，我们按照

B3, B4, B5, A0, A1, A2

的顺序进行DFS，这样就可以达到我们的目的。但事实上这样的顺序太过严格，我们只需要保证被指向的强连通分量的至少一个顶点排在指向这个连通分量的所有顶点前面即可，比如

B3, A0, A1, A2, B4, B5

B3排在了强连通分量A所有顶点的前面。

现在我们的关键问题就是如何得到这样一个满足要求的顶点顺序，Kosaraju 给出了这解决办法：

对原图取反，然后从反向图的任意节点开始进行DFS的逆后序遍历，逆后序得到的顺序一定满足我们的要求。

DFS的逆后序遍历是指：如果当前顶点未访问，先遍历完与当前顶点相连的且未被访问的所有其它顶点，然后将当前顶点加入栈中，最后栈中从栈顶到栈底的顺序就是我们需要的顶点顺序。

上图表示原图的反向。

我们现在进行第一种假设：假设DFS从位于强连通分量A中的任意一个节点开始。那么第一次DFS完成后，栈中全部都是强连通分量A的顶点，第二次DFS完成后，栈顶一定是强连通分量B的顶点。保证了从栈顶到栈底的排序强连通分量B的顶点全部都在强连通分量A顶点之前。

我们现在进行第二种假设：假设DFS从位于强连通分量B中的任意一个顶点开始。显然我们只需要进行一次DFS就可以遍历整个图，由于是逆后续遍历，那么起始顶点一定最后完成，所以栈顶的顶点一定是强连通分量B中的顶点，这显然是我们希望得到的顶点排序的结果。

上面使用了最简单的例子说明 Kosaraju 算法的原理，对于有多个强连通分量，连接复杂的情况，仍然适用。大家可以自行举例验证。

综上可得，不论从哪个顶点开始，图中有多少个强连通分量，逆后续遍历的栈中顶点的顺序一定会保证：被指向的强连通分量的至少一个顶点排在指向这个连通分量的所有顶点前面。所以，我们求解强连通分量的步骤可以分为两步：

对原图取反，从任意一个顶点开始对反向图进行逆后续DFS遍历
按照逆后续遍历中栈中的顶点出栈顺序，对原图进行DFS遍历，一次DFS遍历中访问的所有顶点都属于同一强连通分量。

DFS 生成树

在介绍该算法之前，先来了解 DFS 生成树，我们以下面的有向图为例：

有向图的 DFS 生成树主要有 4 种边（不一定全部出现）：

树边（tree edge）：绿色边，每次搜索找到一个还没有访问过的结点的时候就形成了一条树边。
反祖边（back edge）：黄色边，也被叫做回边，即指向祖先结点的边。
横叉边（cross edge）：红色边，它主要是在搜索的时候遇到了一个已经访问过的结点，但是这个结点并不是当前结点的祖先时形成的。
前向边（forward edge）：蓝色边，它是在搜索的时候遇到子树中的结点的时候形成的。

我们考虑 DFS 生成树与强连通分量之间的关系。

如果结点 u 是某个强连通分量在搜索树中遇到的第一个结点，那么这个强连通分量的其余结点肯定是在搜索树中以 u 为根的子树中。u 被称为这个强连通分量的根。

反证法：假设有个结点 v 在该强连通分量中但是不在以 u 为根的子树中，那么 u 到 v 的路径中肯定有一条离开子树的边。但是这样的边只可能是横叉边或者反祖边，然而这两条边都要求指向的结点已经被访问过了，这就和 u 是第一个访问的结点矛盾了。得证。

Tarjan 算法求强连通分量

引入时间戳的概念

在 Tarjan 算法中为每个结点 u 维护了以下几个变量：

dfn[u]：深度优先搜索遍历时结点 u 被搜索的时间戳(次序)。
low[u]：从 u 开始遍历时, 所能遍历到的最小时间戳时什么. 所以 low[u] 定义为以下结点的dfn 的最小值：Subtree(u) 中的结点；从Subtree(u) 通过一条不在搜索树上的边能到达的结点。一个结点的子树内结点的 dfn 都大于该结点的 dfn。
u是其所在的强联通分量的最高点. 等价于 dfn[u] == low[u]

从根开始的一条路径上的 dfn 严格递增，low 严格非降。

按照深度优先搜索算法搜索的次序对图中所有的结点进行搜索。在搜索过程中，对于结点 u 和与其相邻的结点 v v 不是 u 的父节点）考虑 3 种情况：

v 未被访问：继续对 v 进行深度搜索。在回溯过程中，用 low[v] 更新 low[u]。因为存在从 u 到 v 的直接路径，所以 v 能够回溯到的已经在栈中的结点，u 也一定能够回溯到。
v 被访问过，已经在栈中：即已经被访问过，根据 low 值的定义（能够回溯到的最早的已经在栈中的结点），则用dfn[v] 更新 low[u] 。
v 被访问过，已不在在栈中：说明 v 已搜索完毕，其所在连通分量已被处理，所以不用对其做操作。

时间复杂度 O(n+m) 。

示例

从节点 1 开始DFS，把遍历到的节点加入栈中。搜索到节点 u=6 时，DFN[6]=LOW[6]，找到了一个强连通分量。退栈到 u=v 为止，{6}为一个强连通分量。

初始化时Low[u]=DFN[u]=++index

返回节点5，发现DFN[5]=LOW[5]，退栈后{5}为一个强连通分量。

返回节点3，继续搜索到节点4，把4加入堆栈。发现节点4向节点1有后向边，节点1还在栈中，所以LOW[4]=1。节点6已经出栈，(4,6)是横叉边，返回3，(3,4)为树枝边，所以LOW[3]=LOW[4]=1。

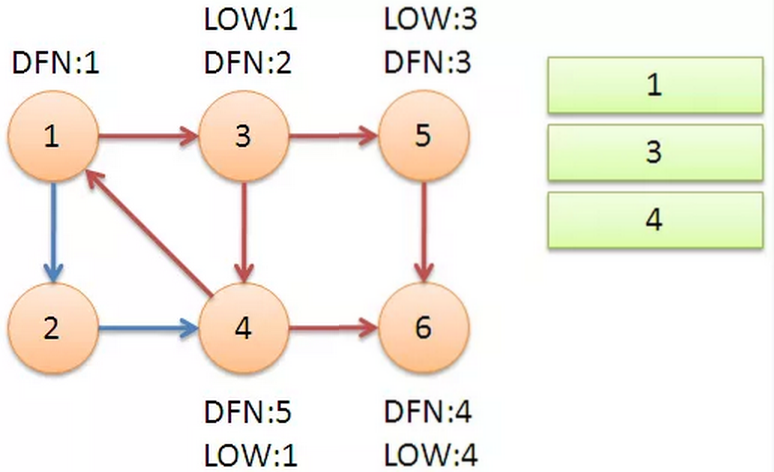
Low(u)=Min {Low(u), DFN(v) } DFN(v),(u,v)为指向栈中节点的后向边

继续回到节点1，最后访问节点2。访问边(2,4)，4还在栈中，所以LOW[2]=DFN[4]=5。返回1后，发现DFN[1]=LOW[1]，把栈中节点全部取出，组成一个连通分量{1,3,4,2}

至此，算法结束。求出了图中全部的三个强连通分量{1,3,4,2},{5},{6}

联通分量递减的顺序就一定是拓扑序.