贪心算法(又称贪婪算法) 是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说不从整体最优上加以考虑，他所做出的是在某种意义上的局部最优解。
贪心的注意点： 贪心算法不是对所有问题都能得到整体最优解，关键是贪心策略的选择。简单地说，贪心就是“走一步看一步”、“只看眼前，不管将来”。对所采用的贪心策略一定要仔细分析其是否满足无后效性，即某个状态以后的过程不会影响以前的状态，只与当前状态有关。
贪心算法的使用前提：局部最优解一定能导致全局最优解。
贪心解决问题过程：
① 建立模型来描述问题。
② 把求解的问题分成若干个子问题。
③ 对每一子问题求解，得到子问题的局部最优解。
④ 把子问题的解局部最优解合成原来解问题的一个解。
贪心策略的选择
因为用贪心算法只能通过解局部最优解的策略来达到全局最优解，因此，一定要注意判断问题是否适合采用贪心算法策略，找到的解是否一定是问题的最优解。
贪心算法的实现框架 ：
从问题的某一初始解出发；
while（能朝给定总目标前进一步）{
利用可行的决策，求出可行解的一个解元素；
}
由所有解元素组合成问题的一个可行解；典型的贪心例子
1. 最优装载问题：给n个物体，第i个物体重量为wi，选择尽量多的物体，使得总重量不超过C。
贪心策略：先装最轻的。
2.部分背包问题：有n个物体，第i个物体的重量为wi，价值为vi，在总重量不超过C的情况下让总价值尽量高。每一个物体可以只取走一部分，价值和重量按比例计算。
贪心策略：先拿性价比高的。
3.乘船问题：有n个人，第i个人重量为wi。每艘船的载重量均为C，最多乘两个人。用最少的船装载所有人。
贪心策略：最轻的人和最重的人配对。
4.选择不相交区间问题：给定n个开区间(ai,bi)，选择尽量多个区间，使得这些区间两两没有公共点。【算法】
首先按照结束时间b1<=b2<=…<=bn的顺序排序，依次考虑各个活动，如果没有和已经选择的活动冲突，就选；否则就不选。
【正确性】
假设bj<bi且(aj,bj)(ai,bi)分别与之前的活动不冲突，如果当前选(aj,bj)，若(aj,bj)(ai,bi)不冲突则还可以选择(ai,bi)，答案加一；若(aj,bj)(ai,bi)冲突，因为bj<bi，所以(aj,bj)对以后的影响更小。
5、区间选点问题：给定n个闭区间[ai, bi]，在数轴上选尽量少的点，使得每个区间内都至少有一个点（不同区间内含的点可以是同一个）。【算法】
首先按照结束位置从小到大排序。然后从区间1到区间n进行选择：对于当前区间，若集合中的数不能覆盖它，则将区间末尾的数加入集合。
贪心策略是：取最后一个。
如下图，如果选灰色点，则移动到黑色点会更优。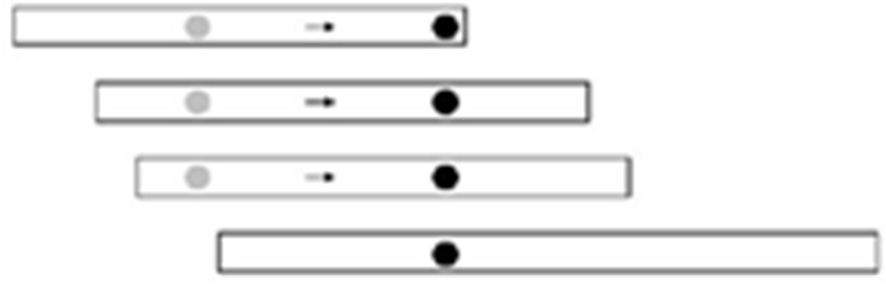
6、区间覆盖问题：给n个闭区间[ai,bi]，选择尽量少的区间覆盖一条指定线段[s,t]。
【算法】
将所有的区间按左端点从小到大排序，依次处理每个区间。每次选择覆盖点s的区间中右端点坐标最大的一个，并将s更新为该区间的右端点坐标，直到选择的区间已包含了t为止。
贪心思想：在某个时刻s，找一个满足a[i]<=s的b[i]最大值即可。
7、流水作业调度问题：问题描述 某工厂收到了n个产品的订单,这n个产品分别在A、B两个车间加工,并且必须先在A车间加工后才可以到B车间加工。 某个产品i在A、B两车间加工的时间分别为ai、bi。怎样安排这n个产品的加工顺序,才能使总的加工时间最短。这里所说的加工时间是指：从开始加工第一个产品到最后所有的产品都已在A、B两车间加工完毕的时间。
【算法分析】
要使时间最短，则就是让机器的空闲时间最短。
B机器在加工过程中，有可能要等待A机器。
最后一个部件在B机器上加工，A机器也在等待B机器的完工。
要使总的空闲时间最少，就要把在A机器上加工时间最短的部件最先加工，这样使得B机器能以最快的速度开始加工；把在B机器上加工时间最短的部件放在最后加工。这样使得A机器能尽快的等待B机器完工。
于是我们可以设计出这样的贪心法：
设Mi=min{ai, bi}
将M按照从小到大的顺序排序。然后从第1个开始处理，若Mi=ai，则将它排在从头开始的作业后面，若Mi=bi，则将它排在从尾开始的作业前面。
8、带限期和罚款的单位时间任务调度 问题：有n个任务，每个任务都需要1个时间单位执行，任务i的截止时间di(1<=di<=n)表示要求任务i在时间di结束时必须完成，误时惩罚wi表示若任务i未在时间di结束之前完成，将导致wi的罚款。 确定所有任务的执行顺序，使得惩罚最小。
【贪心方法】
要使罚款最少，我们显然应尽量完成w[i]值较大的工作。
此时，我们可以将工作按w[i]从大到小进行排序，然后按照排好的顺序依次对工作进行安排，安排的规则为：使处理工作i的时间既在d[i]之内，又尽量靠后；如果d[i]之内的时间都已经排满，就放弃处理此项工作。
贪心是一种每次在决策时采用当前一一下最优策略的算法，使用贪心算法要求问题的整体最优性由局部最优性导出。贪心算法的正确性需要证明，常用手法如下：
1.微扰（邻项交换）
证明在任意局面下，任何对局部最优策略的微小改变都会造成整体结果变差。经常用于以“排序”为贪心策略的证明。
2.决策包容性
证明在任意局面下，做出局部最优策略以后，在问题状态空间的可大集合包含了做出其他任何决策后的可达集合。换言之，这个局部最优策略提供的可能性包含了其他所有决策提供的可能性。
3.决策范围扩展
有时候不容易直接证出局部最优策略的正确性。此时可以往后多扩展出来一步，有助于我们对局部最优决策进行验证（验证时可以综合其他手法）。
4.反证法
5.数学归纳法