特殊数列

等差数列 a_n=a₁+(n-1)×d

等比数列 通项 a_n=a₁*q^n-1 ，其中常数q叫作公比。

例题: 2019 CSP-S 14. 有一个等比数列，共有奇数项，其中第一项和最后一项分别是2和118098, 中间一项是486,请问以下哪个数是可能的公比？（）

 A. 5
 B. 3
 C. 4
 D. 2

答案：「B」 试题分析: 486 / 2 = 243, 118098 / 486 = 243，243 =  3⁵ 所以只有3符合要求.

常见数列：

斐波那契数列 F_i=F_i-1+F_i-2，  F₁=F₂=1 的数列 {Fn} 称为斐波那契数列，为斐波那契数

Catalan 卡特兰数列

递推公式：

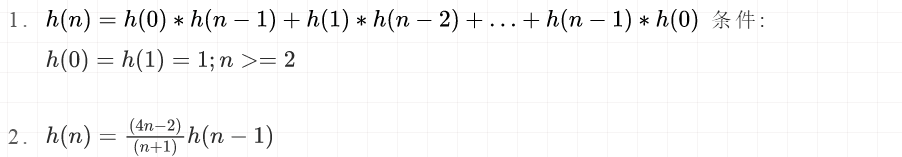
应用:

1. 出栈序列数

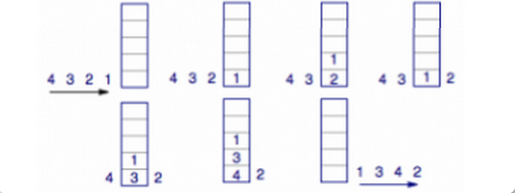
2. 二叉树构成 n个结点, 问能构成几种不同的二叉树
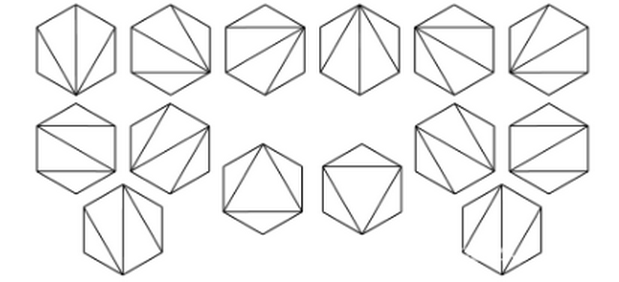
3. n+2 条边的凸多边形的三角形划分

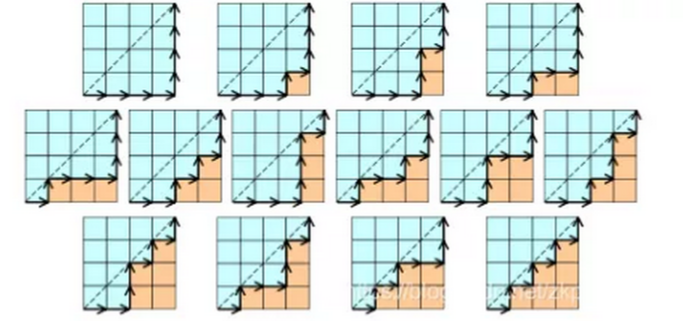
4. 在n*n的格子中，只在下三角行走，每次横或竖走一格，有多少种走法？

5. 由n对括号形成的合法括号表达式的个数为
6. n+1个数连乘，不同的乘法顺序数为

第二类斯特林数

第二类斯特林数 「S(n,m)」 表示的是把n个不同的小球放在m个相同的盒子里方案数(盒子不为空)。

递推:

S(n,m)=S(n-1,m-1)+m*S(n-1,m)

• 第n个球单独放入一个盒子里, 剩下的n-1个球放入m-1个盒子里S(n-1,m-1)
• 第n个球不单独放入一个盒子里, 剩下的n-1个球放入m个盒子里, 盒子不能空, 那么第n个球可以放在任一盒子里, 所以有m*S(n-1,m)

第一类斯特林数

将n个不同的元素划分为k个圆排列的方案数.

递推式:f(i,j)=f(i-1,j-1)+(i-1)*f(i-1,j)

加入一个新的数有两种情况:

1. 是自己成环, 剩下的 i-1 个数形成 j-1 个环
2. 是加入以前的环，那么这个数可以插到任何一个数的前面 (i−1) f(i−1, j)

Catalan数

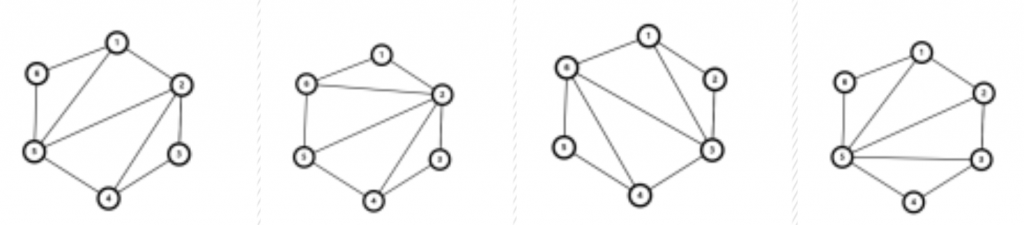
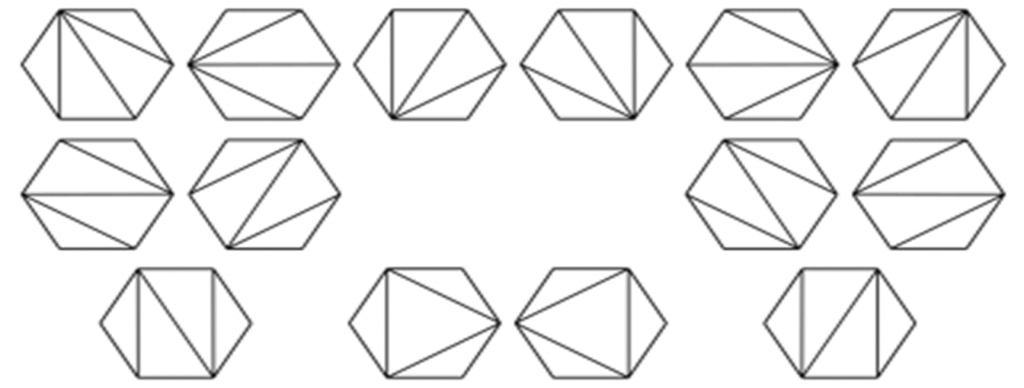
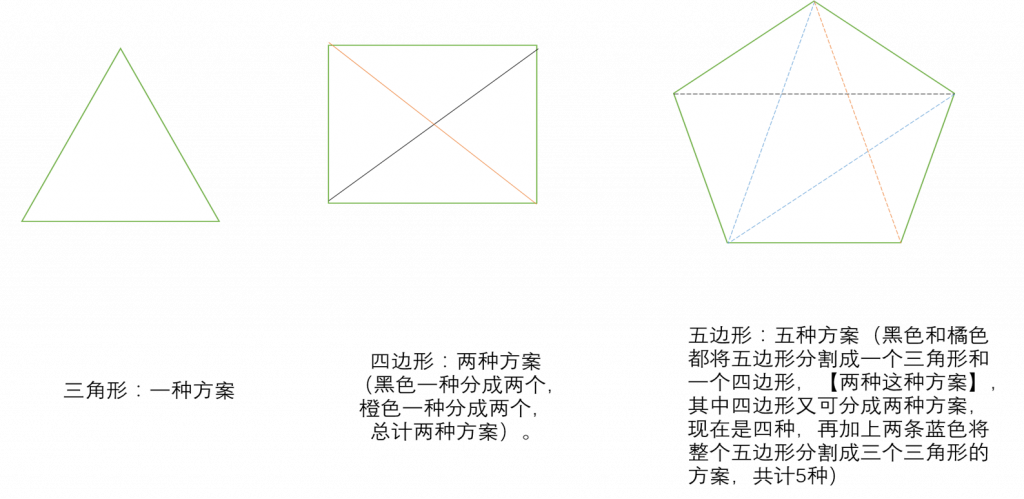
Catalan数列的应用

第二类斯特林数