1、基本概念
欧拉路指的是:存在这样一种图,可以从其中一点出发,不重复地走完其所有的边。 如果欧拉路的起点与终点相同,则称之为欧拉回路。
其实就是-笔从起点经过所有边到达终点(欧拉路)和一笔从起点经过所有边回到起点(欧拉回路)。
2、如何判断是否有回路
(1)无向图
结论:度数为偶数
证明:为了使形成回路,必定进入节点后,必须出去连接下一点(也就是说,进入节点多少次,就要出节点多少次)。
如果存在奇数条边,那么,必定总有一条边只可以进入节点而不可以出去和其他节点连接,就导致不可以构成回路。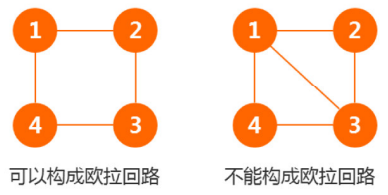
(2)有向图
结论:出度与入度相等
证明:同理,多少边进入,就要有多少边出去。
3、判断是否有欧拉路径
和欧拉回路类似:
(1)无向图中,除起点终点是奇数条边,其余度数全都是偶数。
(2)除起点和终点以外,出度和入度相等,起点出度比入度大1,终点入度比出度大。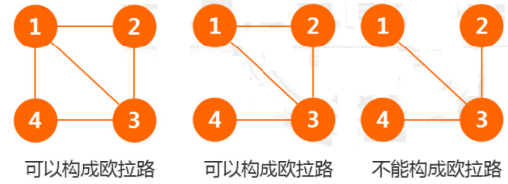 总结:
总结:
(1)无向图能构成欧拉路:有2个或0个奇点;
(2)有向图能构成欧拉路:除起点和终点外,其余点出度和入度相等。(起点出度=入度+1,终点入度=出度+1,也可以出度==入度)
备注:当然,首先需要图是连通图。
分类
