一、格雷码 是一种二进制编码，相邻数字仅一位不同。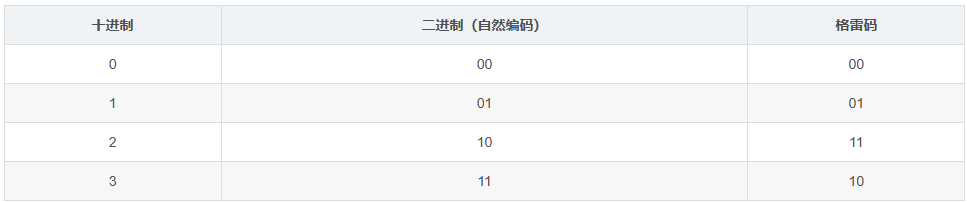
二、格雷码的生成算法：可以通过递归的方式来实现。对于n位格雷码，可以通过生成n-1位格雷码来构造。具体步骤如下：
基础情况：1位格雷码由两个1位二进制串组成，顺序为0和1。
递归生成：对于n位格雷码，首先生成 n-1 位格雷码，然后将其分为两部分（“镜面反射”法）：前2n-1 个二进制串按顺序排列，并在每个串前加一个前缀0；后2n-1个二进制串按逆序排列，并在每个串前加一个前缀1。这样，就得到了n位格雷码。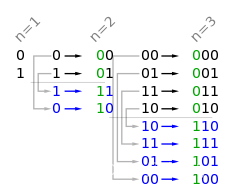
例如上图，
2位格雷码可以这样推出：
已知1位格雷码为0和1，前两个格雷码为00和01，后两个格雷码为11和10，合并得到00，01，11，10。
同理，3位格雷码可以这样推出：已知2位格雷码为00，01，11，10，前四个格雷码为000，001，011，010，后四个格雷码为110，111，101，100，合并得到000，001，011，010，110，111，101，100。
三、格雷码的性质包括：
❶、任意两个相邻的代码只有一位二进制数不同，称为反射码或循环码；
❷、最大数与最小数之间也仅一位数不同，称为首尾相连。
这些性质使得格雷码在通信和测量技术中得到广泛应用，因为它可以减少错误的发生。
1、下面有关格雷码的说法，错误的是（ ）。
A. 在格雷码中，任意两个相邻的代码只有一位二进制数不同。
B. 格雷码是一种唯一性编码。
C. 在格雷码中，最大数和最小数只有一位二进制数不同。
D. 格雷码是一种可靠性编码。
答案：B 格雷码的编码不是唯一的编码。任意 两个相邻的代码只有一位二进制数不同 ,则称这种编码为格雷码。所以不是唯一性编码。
2、3 位格雷编码的正确顺序是（ ）。
A. 000, 001, 010, 011, 100, 101, 110, 111
B. 000, 001, 011, 010, 110, 111, 101, 100
C. 000, 010, 001, 011, 100, 110, 101, 111
D. 000, 010, 110, 100, 111, 101, 011, 001
答案：B 格雷码不唯一，相邻的两个编码只有一位不同，只有B满足。
3、以下C++代码实现 位的格雷码，则横线上应填写（ ）。
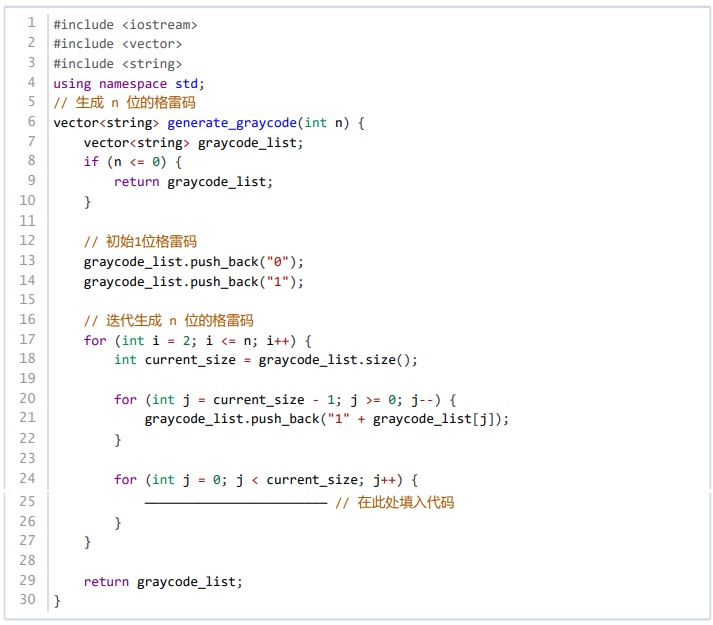
A. graycode_list.push_back(“0” + graycode_list[j]);
B. graycode_list[j] = “0” + graycode_list[j];
C. graycode_list.push_back(“1” + graycode_list[j]);
D. graycode_list[j] = “1” + graycode_list[j];
答案：B 解析：格雷码（Gray code）是一种相邻两个代码之间只有单个比特不同的二进制数字系统。要生成n位的格雷码，可以通过迭代的方式生成更长的格雷码序列。在这段代码中，首先生成了1位的格雷码，即”0″和”1″。然后通过迭代，每次都将现有的格雷码列表翻倍，并且在新加入的格雷码前加上不同的前缀来保证相邻格雷码之间的差异性。在每一轮迭代中，首先将现有的格雷码序列反转并加上前缀”1″，然后原有的格雷码序列加上前缀”0″。
仔细观察，可以看到第一个循环是从末尾向前遍历，将’1’添加到现有元素的前面。这意味着，对于第二个循环，我们应该从头部开始遍历，同样将’0’添加到现有元素的前面，所以选B而不是选A。