一、树链剖分是一种处理树上路径问题的算法技巧。指一种对树进行划分的算法,它先通过轻重边剖分将树分为多条链,保证每个点属于且只属于一条链,然后再通过数据结构(树状数组、BST、SPLAY、线段树等)来维护每一条链。
树链剖分的核心就是如何恰当地将树剖分为若干条链,形成若干个序列,将所有序列按顺序拼接起来后,每条链就成为了一段区间,而序列上的区间问题可以用线段树等数据结构解决。
二、树链剖分主要有两种类型:
1.重链剖分:将树中的边分为重边和轻边,重边连接的节点称为重儿子,轻边连接的节点称为轻儿子。重链由重儿子构成,轻链由轻儿子构成。这种方法在处理树上问题时较为常见。
2.长链剖分:将深度差最大的儿子称为长儿子,将树分成若干条长链。这种方法相对较少使用。
三、树链剖分的几个重要概念:
-重儿子和轻儿子:在节点的所有子节点中,子树节点数目最多的子节点是重儿子,其余子节点是轻儿子。
-重边和轻边:连接节点和它的重儿子的边是重边,连接节点和轻儿子的边是轻边。
-重链:由重边连接而成的路径叫重链。
-整棵树会被剖分成若干条重链。
-轻儿子一定是每条重链的顶点。
-任意一条路径被剖成不超过log2n条链。
•我们将树中的边分成重边和轻边。如下图,加粗的边是重边,其余是轻边。 我们可以以任意点为根,然后记size(u)为以u为根的子树的结点个数,令 v 为 u 所有儿子中 size 值最大的一个儿子,则 (u,v) 为重边,v 称为 u 的重儿子。 u 到其余儿子的边为轻边
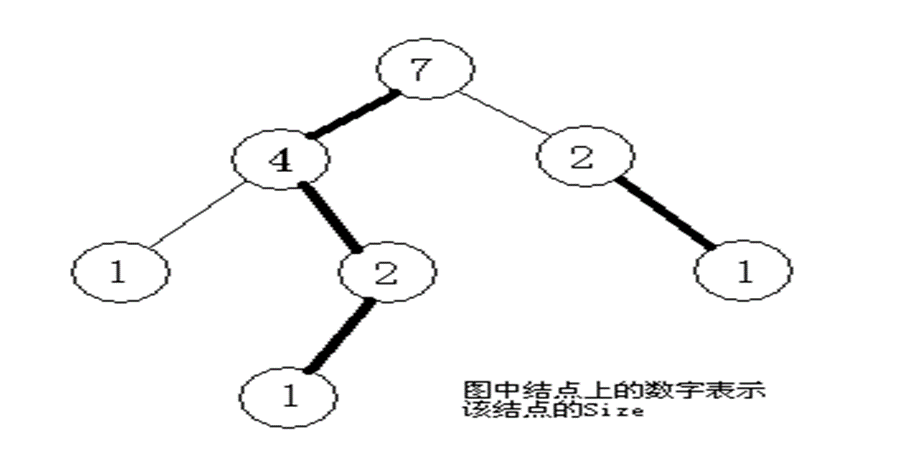
轻重边的性质:
•性质1:如果(u,v)为轻边,则 size(v)≤size(u)/2 。
•性质2:从根到某一点 v 的路径上的轻边个数不大于O(logn)。
•性质3:我们称某条路径为重路径(链),当且仅当它全部由重边组成。那么对于每个点到根的路径上都有不超过O(logn)条轻边和 O(logn)条重路径。
•容易发现,一个点在且只在一条重路径上,而每条重路径一定是一条从根结点方向向叶结点方向延伸的深度递增的路径。
•考虑操作所给出的路径(u,v) ,我们可以分别处理u,v 两个点到其最近公共祖先的路径。根据性质3,路径可以分解成最多O(logn)条的重路径和最多O(logn) 的轻边,那么现在我们只考虑如何维护这两种对象。
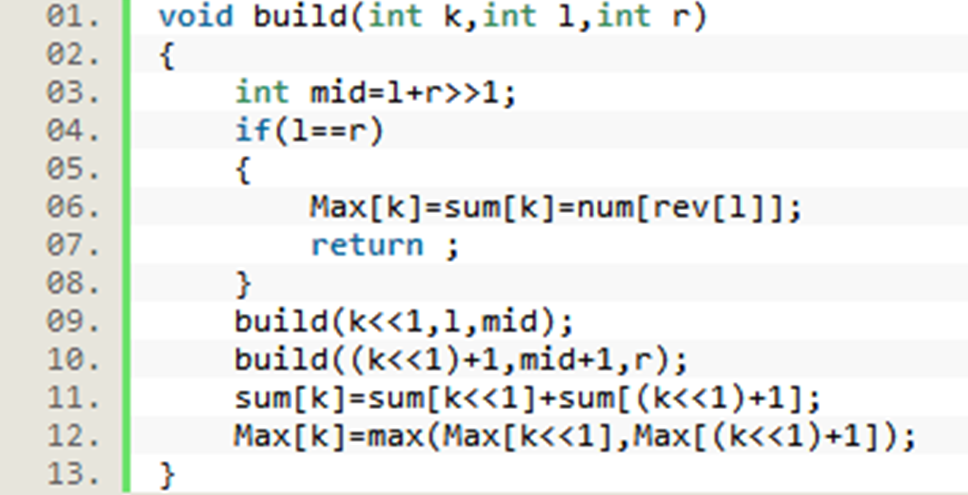
•重路径相当于一个序列,因此只要用线段树来维护。而轻边可以直接跳过,访问下一条重路径,因为轻边的两端点一定在某两条重路径上。这两种操作的时间复杂度分别为O(log2n)和O(logn) ,因此总复杂度即为O(log2n) 。
实现细节:
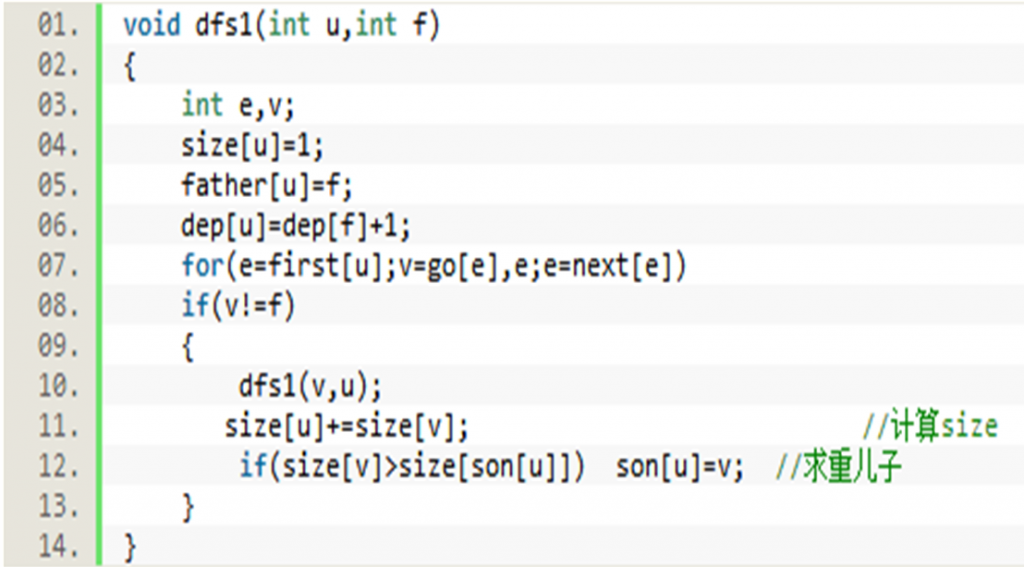
•轻重边剖分的过程可以使用两次dfs来实现。
•剖分过程中要计算如下7个值:
father[x]:x在树中的父亲
size[x]:x的子树结点数(子树大小)
dep[x]:x在树中的深度
son[x]:x的重儿子,即为重边
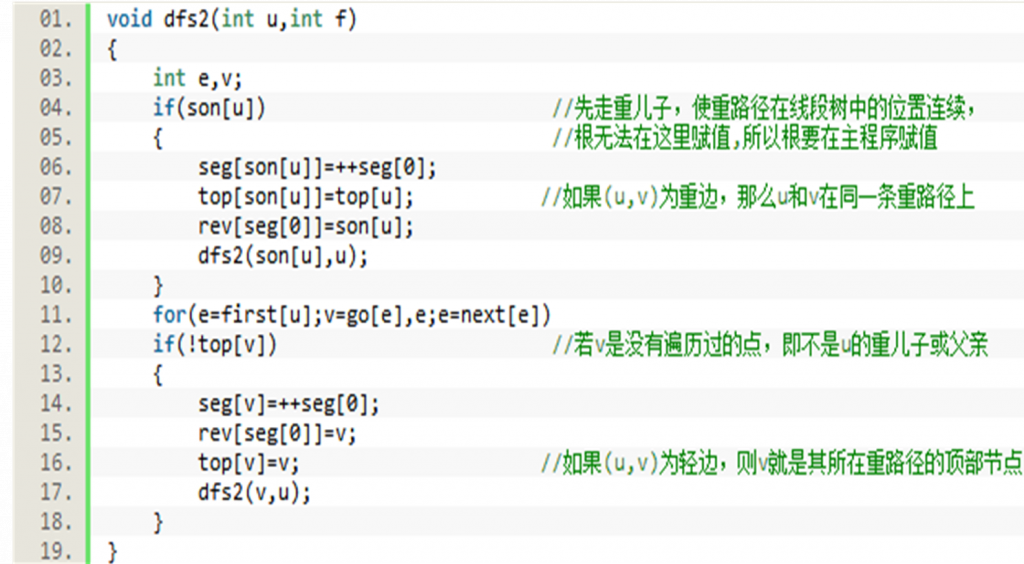
top[x]:x所在重路径的顶部结点(深度最小)
seg[x]:x在线段树中的位置(下标)
rev[x]:线段树中第x个位置对应的树中结点编号,即rev[seg[x]]=x
•第一遍dfs时可以计算前四个值,第二遍dfs可以计算后三个值。而计算seg时,同一条重路径上的点需要按顺序排在连续的一段位置,也就是一段区间。
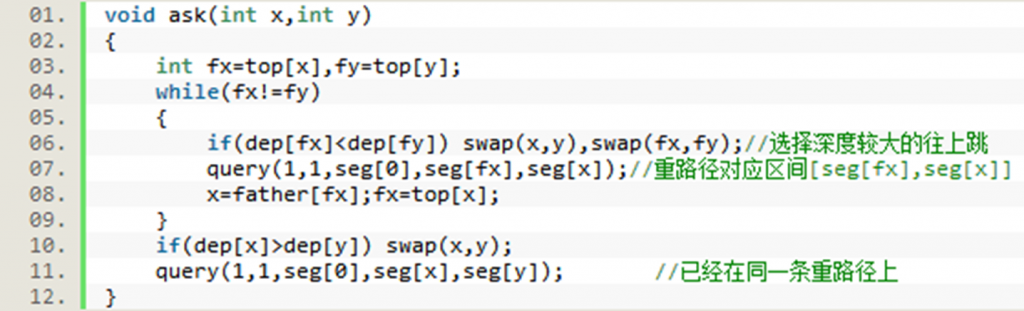
•考虑将一条路径 拆分为若干条重路径:实际上就是寻找最近公共祖先的过程。考虑暴力的做法,我们会选择 中深度较大的点向上走一步,直到 。
•现在有了重路径,由于我们记录了top和seg,因此我们不需要一步步走。假定top[u]和top[v]不同,那么他们的最近公共祖先可能在其中一条的重路径上,也可能在其他的重路径上,因为LCA显然不可能在top深度较大的那条重路径上,所以我们先处理top深度较大的。
•首先我们找出 u,v 中top深度较大的点,假设是u,则我们可以直接跳到 father[top[u]] 处,且跳过的这一段,在线段树中是一段区间,若我们按照深度从小到大来存储点,则这段区间为:[seg[[top[u]],seg[u]]。
•而当 u,v 的top相同时,说明它们走到了同一条重路径上了,这时它们之间的路径也是序列上的一段区间,且中深度较小的那点是原路径的LCA。