树状数组 – 红栗

树状数组（Binary Indexed Tree, BIT），利用数的二进制特征进行检索的一种树状结构。一种真正的高级数据结构：二分思想、二叉树、位运算、前缀和。
主要用于：数组的单点修改、区间求和。查询和修改复杂度都为log₂n。高效！代码极其简洁！
在使用前缀和求区间和的算法中，如果可以做到在0(1)的时间复杂度内查询任意的区间和，但是如果要修改其中一个点的值，那么需要修改一遍前缀和数组，修改的时间复杂度是 0(n)。

1、树状数组拆分原理 根据任意正整数关于2的不重复次幂的唯一分解性质，我们也可以把一串序列表示成一系列子序列的和。
釆用这个想法，我们可将一个前缀和划分成多个子序列的和，而划分的方法与数的2的幂和具有极其相似的方式。
比如：整数21的对应的2进制是10101,对应计算=2⁴ + 2² + 2¹,因此一个长度为21的数组，可以拆分为三段：
（1）长度为2⁴的小区间[1，2⁴] 即[1，16]。
（2）长度为2²的小区间[2⁴+1，2⁴+2²] 即[17，20]。
（3）长度为2⁰的小区间[2⁴+2²+1，2⁴+2²+2⁰] 即[21，21]。
对于区间[1，x]，树状数组将其分为不超过logx个子区间，从而满足快速询问区间和。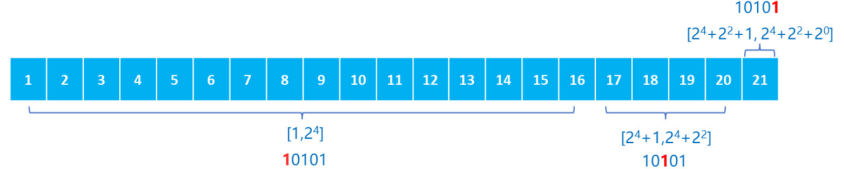

子序列的个数是其二进制表示中1的个数。
根据该理论，一个长度为len的区间可以釆用上述思想划分为log₂len 个子区间。
从右向左看，每个区间的大小其实是len对应二进制的最后一个1的2的次幂。

2、如何求整数x对应二进制的最后一个1往后的值？
lowbit(x)：代表x对应2进制的从最后一位1开始向后构成的值。
例如：
lowbit(10)：返回二进制的 10，即十进制的2。
lowbit(40)：返回二进制的 1000，即十进制的8。
计算方法：
假设 x = 270，对应的2进制为：10111000。
先将 x取反=01000111，再 +1=01001000，此时发现这个值和原来的x对应的 2进制，最后一个1向后的值一致，前面的值正好相反，只要拿这两个值做&运算，结果就是 lowbit(x)的值。
在计算机中，负数是以补码的形式存储的，补码就是数值位取反+1的过程。
因此：lowbit(x) = x & (~x + 1) = x & -x

3、树状数组的划分方法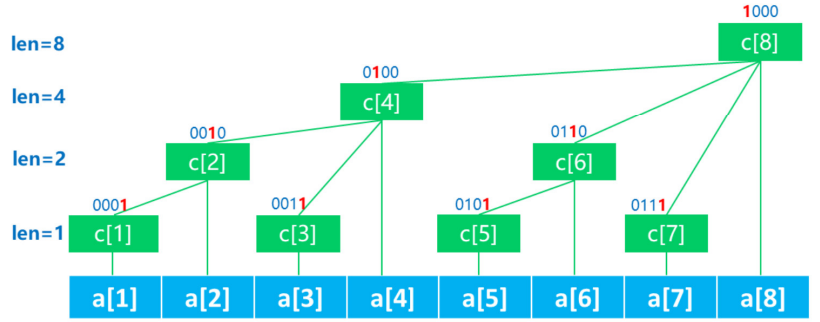
（1）、以a[x]结尾的区间，区间长度为x的最后一个1所对应的2的次幂。
（2）、设定c[x]表示：a数组中，长度为lowbit(x)的区间和，所管理的区间为[x- lowbit(x)+l,x]。
（3）、该结构的特点：
a. 除树根外，结点x的父结点=x+lowbit(x)；
b.长度为n的数组a，所构建的树的深度=log(n)。
注意：树状数组的下标必须从1开始，如果从0开始，lowbit(0)= 0，出现死循环。

4、树状数组修改元素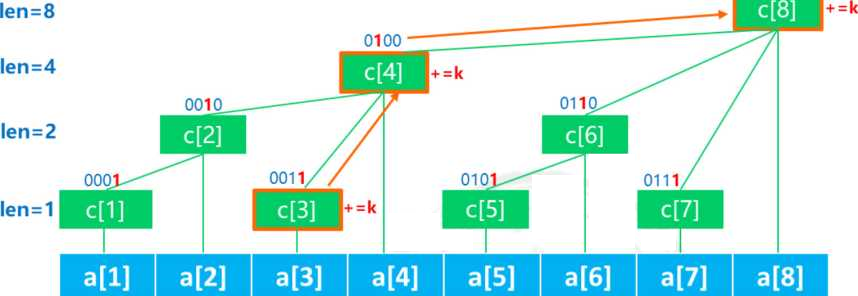

void update(int x,int k){//在数组a的第x个数字上增加数字k
    for(int i=x; i<=n; i=i+lowbit(i)) c[i]+=k;
}

5、树状数组求前缀和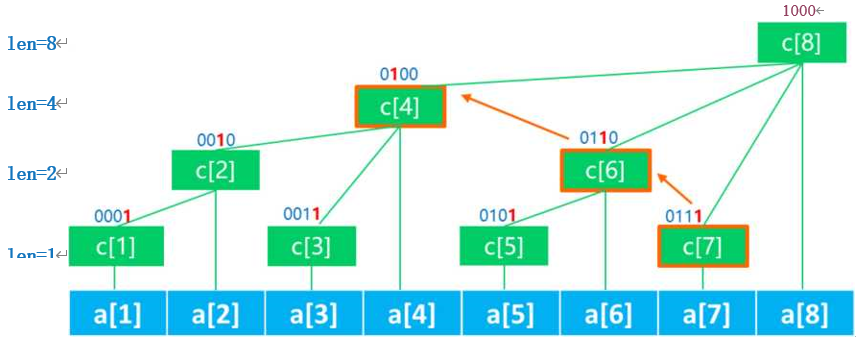

int sum(int x){//求数组[1,x]的所有数字的和
    int ans = 0;
    for(int i=x;i>0;i=i-lowbit(i)) ans+=c[i];
    return ans;
}

特别注意：要注意树状数组能处理的是下标为1..n的数组，绝对不能出现下标为0的情况。因为lowbit(0)=0，这样会陷入死循环。

6、二维树状数组 二维树状数组，其实就是一维的树状数组上的节点再套个树状数组，就变成了二维树状数组了。

int lowbit(int x){
    return x&-x;
}
void update(int x,int y,int v){//单点x,y修改
    for(int i=x;i<=n;i+=lowbit(i))
        for(int j=y;j<=m;j+=lowbit(j)) 
            c[i][j]+=v;
}
long long sum(int x,int y){//从1,1到x,y的二维区间和
    long long res=0;
    for(int i=x;i;i-=lowbit(i))
        for(int j=y;j;j-=lowbit(j))
            res+=c[i][j];
    return res;
}

(x1,y1)~(x2,y2)的二维区间和：sum(x2,y2)-sum(x2,y1-1)-sum(x1-1,y2)+sum(x1-1,y1-1));