树上差分有什么作用？如果对树上的一段路径进行操作，并询问某个点或某条边被经过的次数，树上差分就可以派上用场了。这就是树上差分的基本操作。
树上差分 利用差分的性质，对路径上的重要节点进行修改（而不是暴力全改），作为其差分数组的值，最后在求值时，利用 dfs 遍历求出差分数组的前缀和。树上差分时需要先计算 LCA。
树上差分思想和一维二维差分一样，只不过最后计算前缀和的时候不同。树上差分的计算前缀和 C[i] = C[i]+（其子树的所有节点的C），也就用dfs再跑一次树求和。还有一点值得注意的就是，对点和边的树上差分原理相同，实现略有不同点权差分和边权差分有些许不同。
在使用树上差分之前，首先需要了解树的以下两个性质：
（1）任意两个节点之间有且只有一条路径。
（2）根节点确定后，一个非根节点只有一个父亲节点。
如果我们要考虑从 u 到 v 的路径，u 与 v 的 lca 是 a。那么很明显，如果路径中有一点 u′ 已经被访问了，且 u′≠a，那么 u’ 的父亲也一定会被访问，这是根据以上性质可以推出的。所以，我们可以将路径拆分成两条链，u->a 和 a->v。
点差分
设将两点u,v之间路径上的所有点权增加x，则操作如下：
d[u]+=x;
d[v]+=x;
d[lca(u,v)]-=x;
d[f[lca(u,v)][0]]-=x;
举个例子：设原树如下，现要将2,3之间路径上的所有点的权值增加3，设原权值均为0。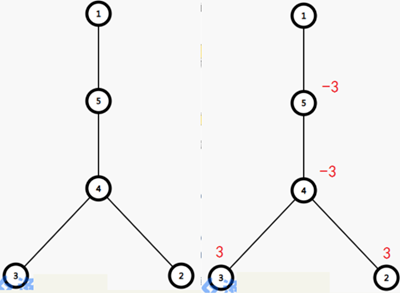
这样，只要dfs一遍，遍历时统计以每个节点为根的树的节点的权值和，就是当前节点的最终权值。
边差分
设将两点u,v之间路径上的所有边权增加x，以每条边两端深度较大的节点存储该边的差分数组，则操作如下：
d[u]+=x;
d[v]+=x;
d[lca(u,v)]-=2*x;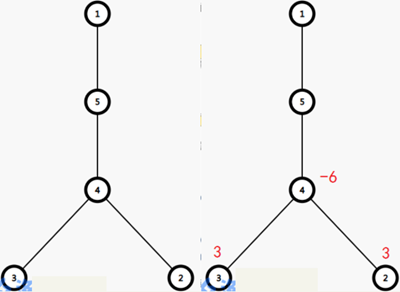
同样地，只要dfs一遍，遍历时统计以每个节点为根的树的节点的权值和，就是当前节点到父亲节点的边的最终权值了。