一．常见的数据结构
(1)集合 集合是由一组无序且唯一(即不能重 复)的项组成的。不包含任何元素的集合就叫做空集。
(2)线性结构 线性结构是一个有序数据元素的集合。常用的线性结构有：线性表，栈，队列，双端队列，数组，串。
(3)树形结构 n 个有限节点组成一个具有层次关系的集合。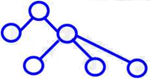
(4)图形结构 多个对多个。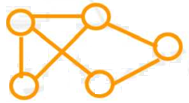
二．什么是树？
树：是一种数据结构，它是由n (n>=0)个有限 节点组成一个具有层次关系的集合。树是一类非线性 结构。这种结构结点之间有分支，并具有层次关系。 它非常类似于自然界中的树。
树的作用：表达家谱顺序、行政组织结构、计算机文件结构、书的教材章节结构等。如下图，一个家族的结构：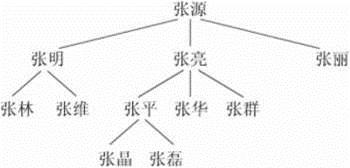
三．树的基本概念
(1) 树是n (n≥０)个结点的有限集。
(2) 当n=0时称为空树；
(3) 当n>0时为非空树，在任意一棵非空树中，有且仅有一个称为根的结点,其余的结点 可分为m(m 30)个互不相交的有限集Ti,T2,…;Tm,其中每一个集合又称为一棵树，并且称为根的子树；同理，每一棵子树又可以分为若干个互不相交的有限集……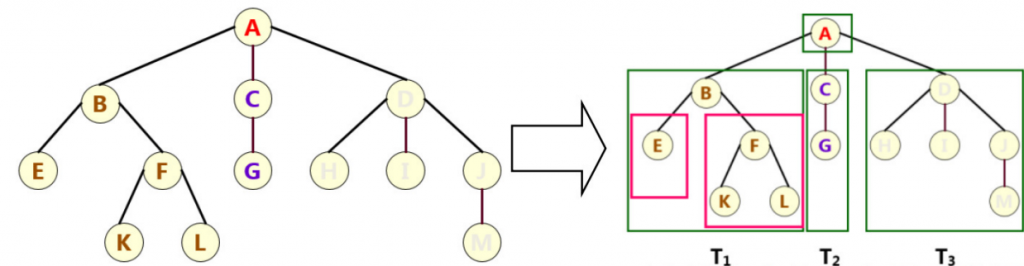
四、总结树的特性：
(1) 空树是树的特例。
(2) 非空树中至少有一个结点，称为树的根，只有根结点的树称为最小树。
(3) 含有多个结点的树中，除根结点外，其余结点构成若干棵子树，且各子树间互不相交。
四．树的基本术语
(1) 树的结点：包含一个数据元素及若干个指向其子树的分支；
(2) 结点的度： 一个结点拥有的子树数目；
(3) 树的度：一棵树上所有结点度的最大值；
(4) 叶子结点(终端结点)：度为零的结点；
(5) 分支结点(非终端结点)：度大于零的结点；
(6) 路径(从根到结点的)：由从根到该结点所经分支和结点构成；
(7) 孩子结点：结点的子树的根称为该结点的孩子结点；
(8) 双亲结点：相应地，该结点称为孩子的双亲结点；
(9) 兄弟： 具有同一父结点的子结点互称兄弟；
(10) 堂兄弟：其双亲在同一层的结点互为堂兄弟；
(11) 祖先结点：从根到该结点所经分支上的所有结点；
(12) 子孙结点：以某结点为根的子树中任一结点都称为该结点的子孙；
(13) 结点的层次： 从根结点到该结点所经过的路径长度加1 ;
(14) 树的深度：树中叶子结点具有的最大层次数；
(15) 树的宽度：整棵树中某一层中最多的结点数称为树的宽度；
(16) 有序树：如果将树中结点的各子树看成从左至右是有次序的(即不能互换)，则称该树为有序树，与之相对的是无序树；
(17) 第一个孩子：在有序树中，最左边的子树的根称为第一个孩子；
(18) 最后一个孩子：在有序树中，最右边的子树的根称为最后一个孩子;
练习：参照下图的树，回答下列问题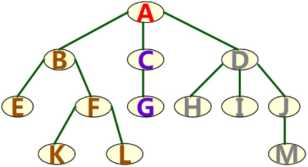
(1) 该树有哪些结点 ABCDEFGHIJKLM, 其中的叶子节点有 EKLGHIM ,分支节点有 ABCDFJ 。
(2) 结点A的度为3 ,结点B的度为2 ,树的度为 3 。
(3) 请写出A节点到K节点经过的路径 A->B->F->K________ 。
(4) H结点的兄弟结点有 I、J ,堂兄弟结点有________。
(5) F结点的祖先结点有 B、A ,子孙结点有 ________ 。
(6) 该树的深度为 4 ,树的宽度为 6 。
五．树的表示方法
（1）双亲表示法
我们假设以一组连续空间存储树的结点，同时在每个结点中，附设一个指示器指示其双亲结点在链表中的位置。也就是说，每个结点除了知道自己是谁以外，还知道它的双亲在哪里. 这样的存储结构，我们可以根据结点的 parent 指针很容易找到它的双亲结点，所用的时间复杂度为 〇(1)，直到 parent 为 -1 时，表示找到了树结点的根。
「优点：」 该存储方式根据结点的 parent 指针很容易找到它的双亲结点，时间复杂度为 O(1)。
「缺点：」 如果需要知道某个结点的所有孩子，需要遍历整棵树。
（2）孩子表示法
「缺点：」 如果需要知道某个结点的双亲，需要遍历整棵树
「改进：」 孩子兄弟表示法
（3）双亲孩子表示法
（4）孩子兄弟表示法
「优点：」 可以把一棵复杂的树变成一棵二叉树，这样就可以充分利用二叉树的特性和算法来处理这棵树了。