如果一个有向图不存在环，也就是任意结点都无法通过一些有向边回到自身，那么称这个有向图为有向无环图。英文名叫 Directed Acyclic Graph，缩写是 DAG。
对一个有向无环图 G 进行拓扑排序，是将 G 中所有顶点排成一个线性序列，使得图中任意一对顶点 u 和 v ，若边<u,v> ∈ E(G)，则 u 在线性序列中出现在 v 之前。通常，这样的线性序列称为满足拓扑次序(Topological Order)的序列，简称拓扑序列。简单的说，由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。
拓扑排序的性质：
（1）、能拓扑排序的图，一定是有向无环图。
（2）、如果有环，那么环上的任意两个节点在任意序列中都不满足条件了。
（3）、有向无环图，一定能拓扑排序。
如何判定一个图是否是有向无环图呢？检验它是否可以进行 拓扑排序 即可。
拓扑排序有何作用？拓扑排序主要用来解决有向图中的依赖解析（dependency resolution）问题。
游戏升级的先后顺序就是一个拓扑序。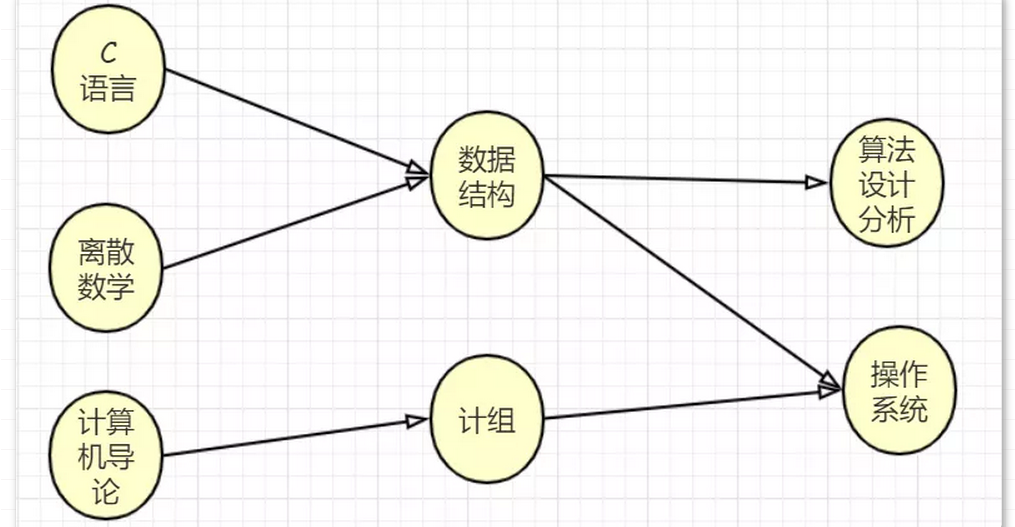
用计算机专业的几门课程的学习次序来描述拓扑关系 ，显然对于一门课来说，必须先学习它的先导课程才能更好地学习这门课程，比如学数据结构必须先学习C语言和离散数学，而且先导课程中不能有环，否则没有尽头了。
拓扑排序的结果不唯一，比如“C语言”和“离散数学”就可以换下顺序，又或者把“计算机导论”向前放在任何一个位置都可以。总结一下就是，如果某一门课没有先导课程或是所有的先导课程都已经学习完毕，那么这门课就可以学习了。
拓扑排序的操作方法：入度表算法（也叫BFS算法或Kahn算法）Kahn算法又叫做入度表算法，算法步骤如下：
1、找出入度为0的点。入度为0，就是没有有任何节点指向它。
2、将这些点的出边删除，也就是这些点指向的目的顶点入度-1，于是就有了新的入度为0的点产生。
3、新的入度为0的点继续执行步骤二，直到不再存在入度为0的点。如果顶点全部被处理完了，那么拓扑排序也就结束了；如果还有顶点没有处理完，那么必定存在环路（所以，拓扑排序也是用来判环的方法）。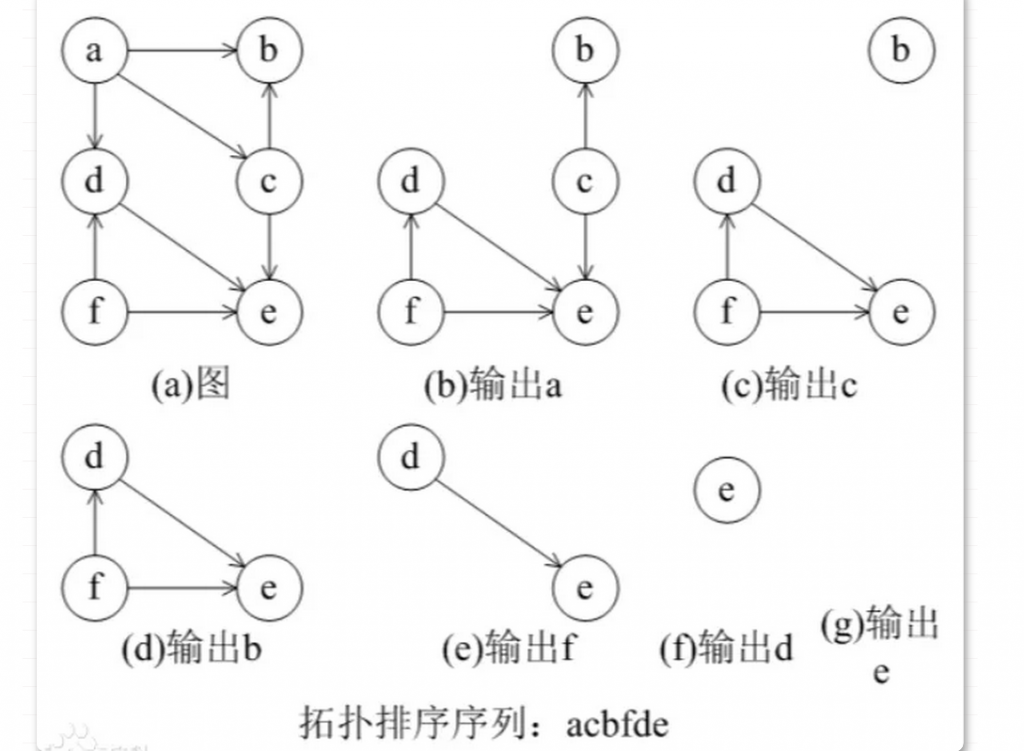
拓扑排序的时间复杂度 如果 DAG 网络有 n 个顶点，m 条边，在拓扑排序的过程中，搜索入度为零的顶点所需的时间是 O(n)。在正常情况下，每个顶点进一次队列，出一次队列，所需时间 O(n)。每个顶点入度减 1 的运算共执行了 m 次。所以总的时间复杂为 O(n+m)。因为拓扑排序的结果不唯一，所以题目一般会要求按某种顺序输出，就需要使用优先级队列，这里采取了最小字典序输出。
🔵 理解拓扑排序基础
首先，要明白拓扑排序解决的是什么问题，以及它本身有哪些特性。
- 核心问题与性质：拓扑排序针对的是有向无环图。它的目的是将图中所有顶点排成一个线性序列，使得对于任何一条有向边 (u, v)，u 在序列中都出现在 v 之前。这意味着排序结果必须满足所有边的方向所定义的先后关系。正因为要满足所有边的方向，如果一个图中存在环（循环依赖），拓扑排序就无法进行。另外，拓扑排序的结果可能不唯一。
- 应用场景：拓扑排序在任务调度、课程安排（如制定考虑先修课关系的课程顺序）、确定编译顺序（如解析软件模块间的依赖关系）等需要处理依赖关系的场景中非常有用。
⚖️ 掌握两种核心算法
Kahn算法和基于DFS的算法是实现拓扑排序最常用的两种方法，它们都基于贪心策略，但侧重点不同。下表对比了它们的主要特点。
| 特性 | Kahn算法（BFS思路） | 基于DFS的算法 |
|---|---|---|
| 核心思想 | “从零入度开始”：不断移除去除了对后续节点影响的、当前入度为0的节点。 | “从终点回溯”：通过深度优先遍历，在递归调用完成后将节点入栈（或逆序添加），利用栈的后进先出特性实现排序。 |
| 关键操作 | 维护一个队列（或栈）来存储当前所有入度为0的节点。 | 在DFS过程中，需要标记节点的状态（如未访问、访问中、已完成）以检测环。 |
| 环检测 | 排序结束后，如果已输出的节点数不等于总节点数，说明图中存在环。 | 在DFS过程中，如果再次访问到状态为“访问中”的节点，说明存在环。 |
| 直观性 | 较为直观，模拟了依赖关系的逐步解除过程。 | 需要理解递归和栈的特性，相对抽象。 |
下面的流程图直观展示了两种算法的步骤，帮助你把握其执行逻辑：
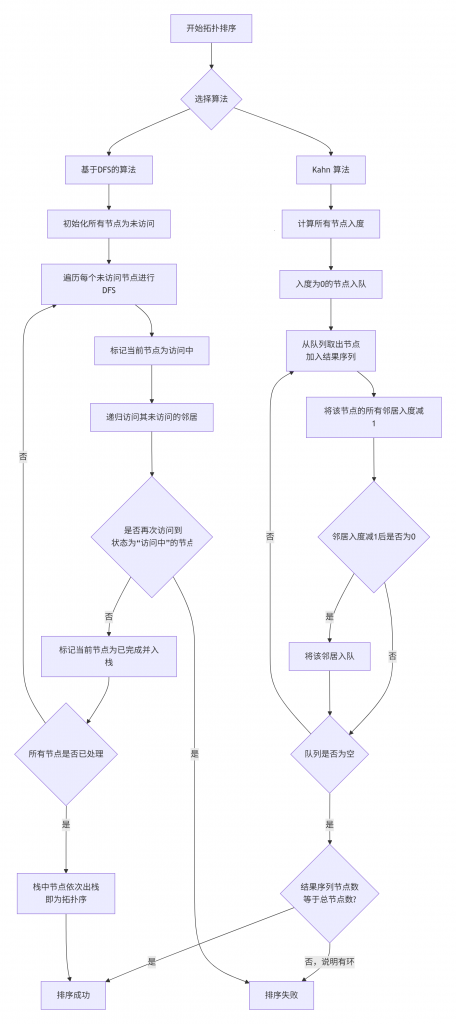
💡 实现要点与进阶技巧
理解算法背后的“为什么”和具体“怎么做”，能让你更扎实地掌握它们。
- 数据结构选择：图的存储结构通常有邻接矩阵和邻接表。对于拓扑排序，邻接表通常是更好的选择，因为它可以高效地遍历一个节点的所有邻居（出边），这在两种算法中都是关键操作，尤其对于边数远小于顶点数的稀疏图，空间效率更高。
- 环检测的实现：这是拓扑排序实现中的一个关键环节。如图表所示，Kahn算法通过最终已排序节点数是否等于总节点数来判断是否有环。而DFS方法则通过维护节点的访问状态（白色-未访问，灰色-访问中，黑色-已完成），如果在DFS过程中访问到一个灰色节点（即当前递归路径上尚未完成回溯的节点），则表明存在环。
- 考虑输出顺序：在某些情况下，我们可能希望输出的拓扑序列是字典序最小（或最大）的。这时，在Kahn算法中，可以使用优先队列（最小堆/最大堆） 来代替普通的队列，每次从队列中取出当前可用的（入度为0的）节点中字典序最靠前或最靠后的那个进行处理。
- 与动态规划结合：拓扑排序可以用于解决AOE网中的关键路径问题，即在DAG中寻找最长路径（通常代表项目的最短完成时间）。方法是在拓扑排序的基础上进行动态规划：设
dp[v]表示从起点到节点 v 的最长路径长度，那么按照拓扑顺序遍历节点，对于每个节点 v，更新其所有邻居 u 的dp[u] = max(dp[u], dp[v] + weight(v, u))。
⚠️ 留意常见陷阱与误区
学习时，注意一些细节，能让你更好地应对复杂情况。
- 图的假设：拓扑排序仅适用于有向无环图 (DAG)。如果图包含环，则无法得到有效的拓扑序列。在实现时，务必加入环检测的逻辑。
- 初始化与状态标记：在DFS实现中，务必确保所有节点的初始状态正确标记为“未访问”。在遍历邻居时，需要根据邻居的状态进行相应判断和处理，例如，只有遇到“访问中”的邻居才说明有环，而遇到“已完成”的邻居则通常无需特殊处理。
- 结果的不唯一性：如前所述，一个DAG可能有多个有效的拓扑序列。例如，当同时存在多个入度为0的节点时，不同的选择会导致不同的序列。除非题目有特殊要求（如输出字典序最小的序列），否则这些序列通常都是正确的。