一、公共祖先：在一棵有根数上，若结点F是结点x的祖先，也是结点y的祖先，那么称F是x、y的公共祖先。
二、最近公共祖先（LCA）：在x、y的所有公共祖先中，深度最大的那个称为最近公共祖先，记为LCA(x, y)。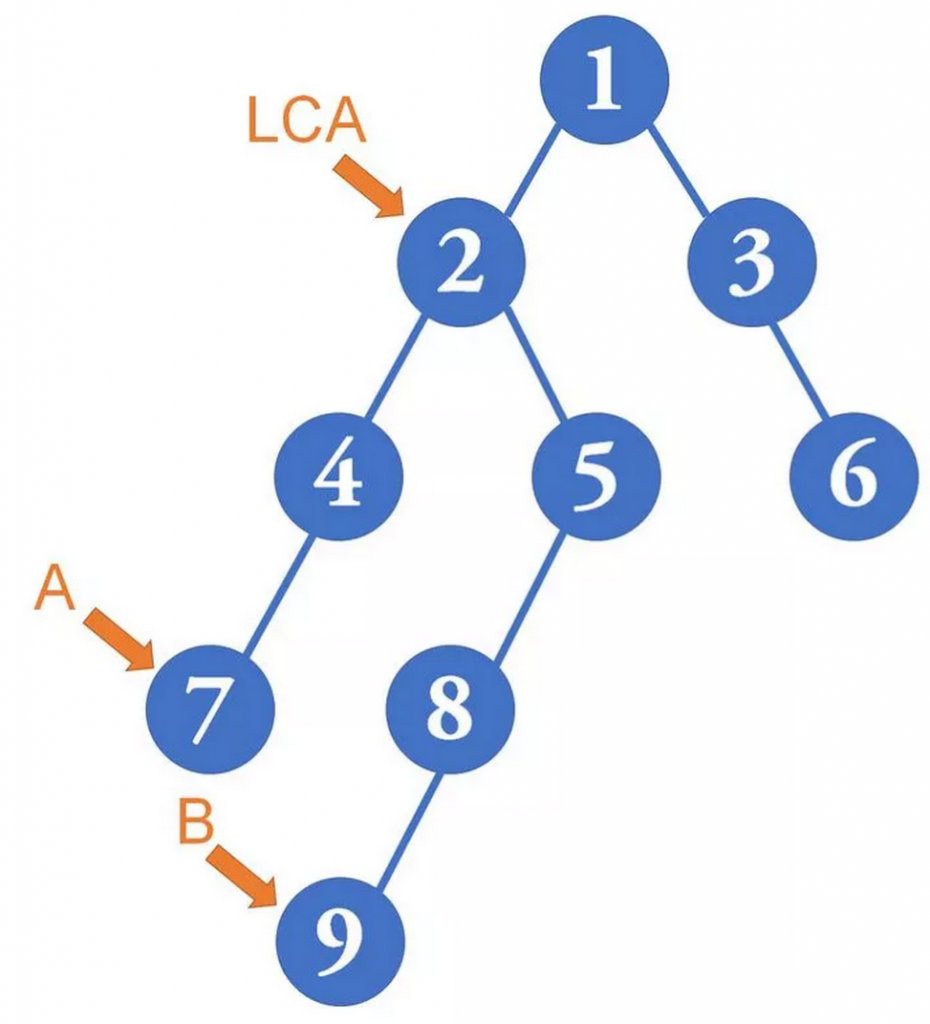
◆ 根结点a的深度是1，每往下一层，深度加1。
◆ 求一棵树上的所有结点的深度，只需要用DFS遍历一次即可。◆ 上图中结点7、9的公共祖先有1、2，其中2的深度是2，1的深度是1，2的深度更大，所以2 = LCA(7, 9)。
三、LCA的性质：
（1）在所有公共祖先中，LCA(x, y)到x和y的距离都最短。
例如在7、9的所有祖先中，2距离7、9最短。
（2）x、y之间最短的路径，经过LCA(x, y)。例如从7到9的最短路径，经过2。
（3）x、y本身也可以是它们自己的公共祖先。若y是x的祖先，则有LCA(x, y) = y，例如图中5 = LCA(5, 9)。
四、求LCA的简单方法：
根据LCA的定义，一个简单直接的方法：
分别从x和y出发，一直往根结点走，第一次相遇的结点，就是LCA(x, y)。
实现用标记法：
◆ 首先从x出发一直向根结点走，沿路标记所有经过的祖先结点；
◆ 把x的祖先标记完之后，然后再从y出发向根结点走，走到第一个被x标记的结点，就是LCA(x, y)。
标记法的复杂度：
高，在有n个结点的树上求一次LCA(x, y)的计算量为O(n)。
若有m次查询，总复杂度是O(mn)，效率太低，
五、标记法的改进：倍增法求LCA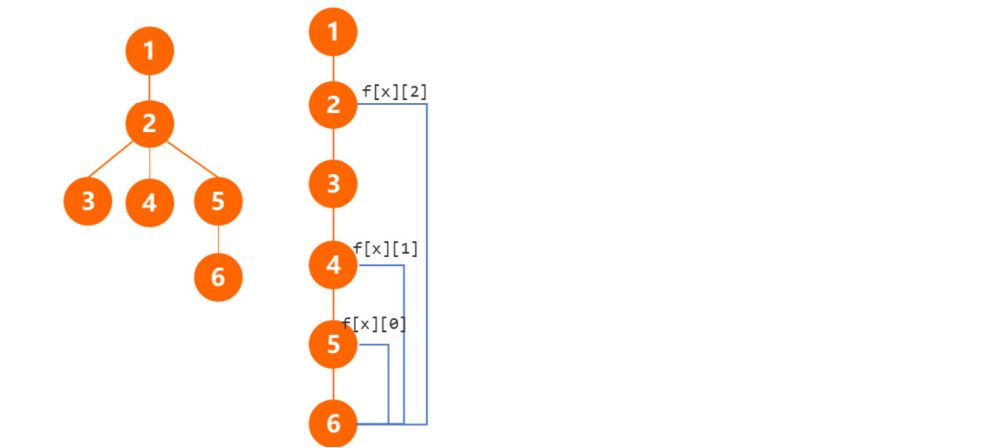
倍增法求解LCA的步骤如下。
(1) 预处理
a. 求深度：对于每个结点dfs预处理出结点深度；
b. 求倍增祖先：计算出每个结点向父元素跳 20，21，22,…,2k 步所到达的结点(在这里2k大于整棵树的最大深度)
备注：
a. 设f[x,k]表示结点x向上跳2k步能到达的祖先，f[x,0]表示x的父元素，如对应 结点不存在f[x,k] = 0。
b. 将路径长度2k分为两半，x跳2k次到的祖先 = x跳2k-1次到的祖先再跳2k-1次。
因此可得：f[x,k] = f[f[x][k-1], k-1]。
c. 有n个结点，每个结点能向上跳的最大次数为logN，因此预处理的时间复杂度为 n*logn。
(2) 查询
对于多次查询结点x和y的公共祖先：
a. 如果x的深度 ＜y 的深度，则交换 xy, 使得 x 更深；
b. 釆用二进制拆分的思想，根据两个结点的深度差，让 x 快速跳转到和 y 一样深；
c. 如果此时x==y,可得 LCA；
d. 如果不相等，釆用二进制拆分的思想，让xy倍增上跳，直到 x 的父和 y 的父相遇 (因为跳出跟以上，f[x][k]=0，因此如果让 x 和 y 相遇，可能结果为0)，可得LCA；
备注：单次查询的时间复杂度为logN。
相关知识点：树上差分