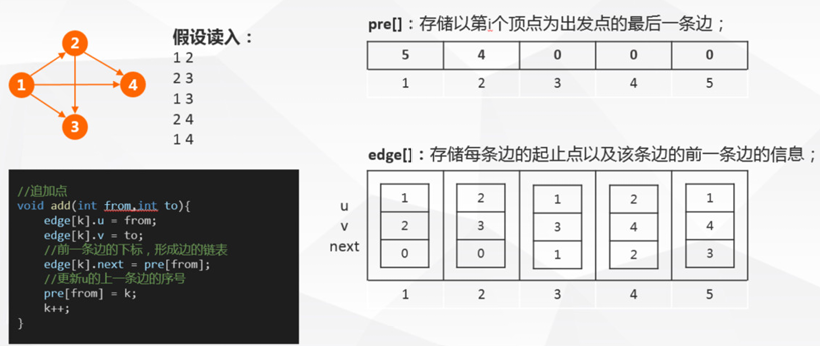
一、最短路算法
从某顶点出发，沿图的边到达另一顶点所经过的路径中，各边上权值之和最小的一条路径叫做最短路径。解决最短路的问题有以下算法：Dijkstra算法，Bellman-Ford算法，Floyd算法 和 SPFA 算法等。
| 特点 | |
| Dijkstra | 用于求单源无负权的最短路。采用贪心思想, 找未访问结点中到源点的最近的点, 然后进行松弛。不能处理 负权边 的情况。 复杂度O(n2) ，使用二叉堆优化可到 O(nlogn)。 |
| Bellman-Ford | 用于求带负权的单源最短路，可判断有无负权回路 (若有则无最短路) 。 n-1 次 对 m 条边松弛。 复杂度O(n*m)。 |
| SPFA | 用于求带负权的单源最短路，可判断有无负权回路，是队列优化的 bellman-Ford。 复杂度O(k*m) (k<n)。 适合稀疏图，但是在稠密图中效率比Dijkstra要低，最恶劣的情况时间复杂度可以到O(n*m)。 |
| Floyd | 用于求多源最短路径、有向图、带负权以及传递闭包，但不能解决负环。 通常用在点比较少的，且起点不固定的问题中。 动态规划 dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]) 复杂度O(n3)。 |
单源最短路: 负权边: SPFA 正权边: 堆优化的dijkstra
多源最短路: Floyd
特别注意：判重 负权回路 INF大小
二、邻接表的存储和遍历：
邻接表又叫链式存储。通常在竞赛中，不使用链表实现，用数组模拟就可以,这种方法称为链式前向星。
前向星是一个特殊的边集数组，通过将边集数组中的每条边按照起点排序（必要时起点相同的边再按终点排序），并记录下以某个点为起点的所有边在数组中的其实位置和存储长度，来构造前向星。
简单来讲，前向星是按照边来存图，而邻接矩阵是按照点来存图。
邻接矩阵适合存储 稠密图，邻接表适合存储 稀疏图。
三、判正(负)环
spfa算法可以在有向图内判正环负环。注意，判负环跑最短路，判正环跑最长路。
SPFA判负环的思路是：当路径经过节点超过n(点数)时，图存在负环。
当我们一直绕着负环走时，由负环定义，该环边权和为负数，我们走的路径权值和是越来小的。所以当图存在负环时，最短路无解(-INF)。若一张图连通，那么它肯定是可以在经过<=n个节点从一点到任意一点的。不存在负环时，一条路径最多经过n个节点；存在负环时，spfa就会一直绕着负环走，经过的节点一定超过n，所以只用判断最短路经过节点点数即可。
还有一种判断负环的方法是记录每个结点加入最短路的次数, 如果一个结点被加入超多n次, 则该结点一定在负环路径上。 不过这种方法的时间复杂度比较高。