关于图的几个概念定义:
连通图:在无向图中,若任意两个顶点vi与vj都有路径相通,则称该无向图为连通图。
强连通图:在有向图中,若任意两个顶点vi与vj都有路径相通,则称该有向图为强连通图。
连通网:在连通图中,若图的边具有一定的意义,每一条边都对应着一个数,称为权;权代表着连接连个顶点的代价,称这种连通图叫做连通网。
生成树:一个连通图的生成树是指一个连通子图,它含有图中全部n个顶点,但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边,如果生成树中再添加一条边,则必定成环。
最小生成树:在连通网的所有生成树中,所有边的代价和最小的生成树,称为最小生成树。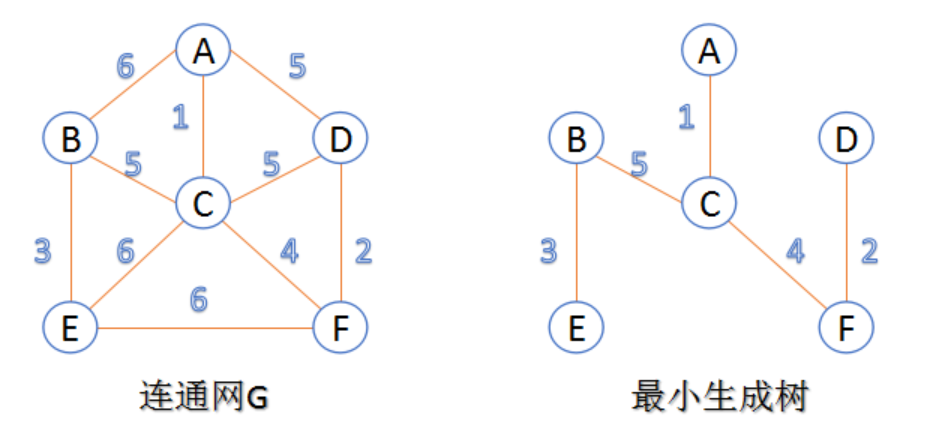
下面介绍两种求最小生成树算法:
1.Kruskal算法
此算法可以称为“加边法”,初始最小生成树边数为0,每迭代一次就选择一条满足条件的最小代价边,加入到最小生成树的边集合里。
(1)、把图中的所有边按代价从小到大排序;
(2)、把图中的n个顶点看成独立的n棵树组成的森林;
(3)、按权值从小到大选择边,所选的边连接的两个顶点ui,vi应属于两颗不同的树,则成为最小生成树的一条边,并将这两颗树合并作为一颗树。
(4)、重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。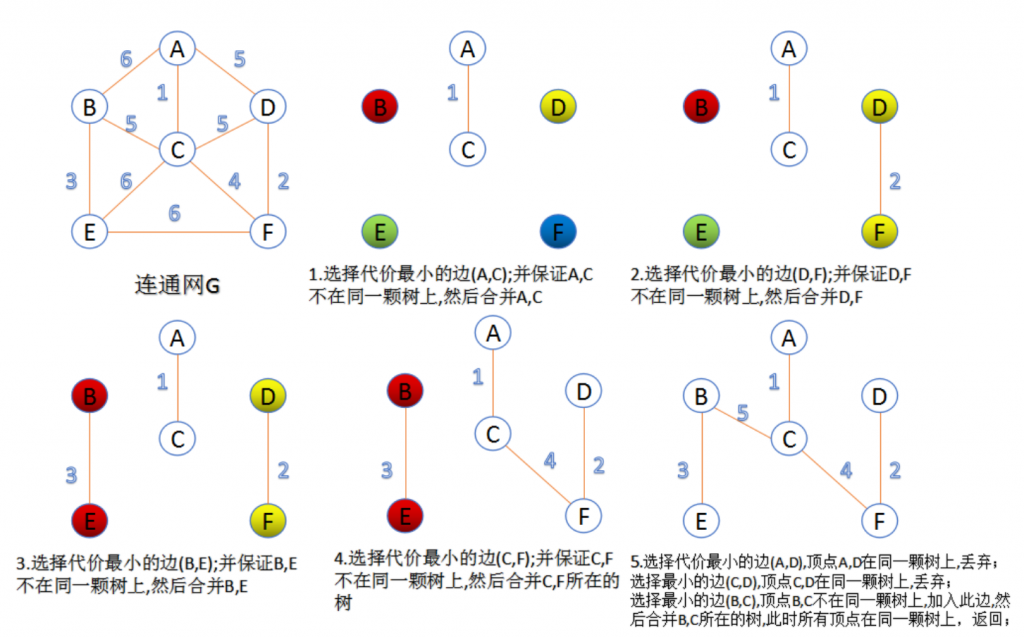
2.Prim算法
此算法可以称为“加点法”,每次迭代选择代价最小的边对应的点,加入到最小生成树中。算法从某一个顶点s开始,逐渐长大覆盖整个连通网的所有顶点。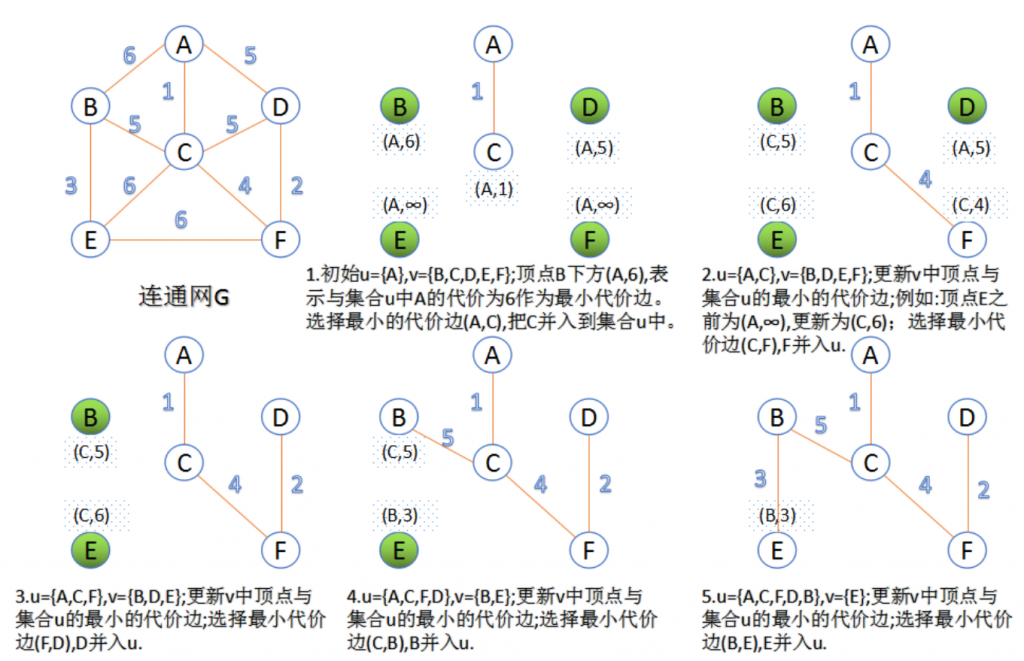
理解最小生成树(MST)确实很重要,它是图论中连接所有顶点且总权值最小的树结构。
🔵 理解最小生成树基础
首先,要明白最小生成树解决的是什么问题,以及它本身有哪些特性。
- 核心问题:在一个带权的无向连通图中,找到一棵子树,这棵树需要包含原图的所有顶点,并且使用的边权值之和最小。
- 关键性质:最小生成树必须是一棵树,因此它必须没有环,并且边数恰好为 顶点数 – 1。另外,最小生成树可能不唯一,但所有最小生成树的边权总和是唯一且最小的。
- 应用场景:最小生成树在通信网络布线、交通道路规划、电路设计等需要以最低成本实现全连通的问题中非常有用。
⚖️ 掌握两种核心算法
Prim算法和Kruskal算法是构造最小生成树最常用的两种方法,它们都基于贪心策略,但侧重点不同。下表对比了它们的主要特点,帮助你理解其核心思想与适用场景。
| 特性 | Prim算法 | Kruskal算法 |
|---|---|---|
| 核心思想 | “加点法”:从单个顶点开始,逐步扩张生成树,每次选择与当前树相连的最小权值边对应的新顶点加入。 | “加边法”:将所有边按权值从小到大排序,逐个尝试添加,若边连接了两个尚未连通的组件(即不形成环)则加入。 |
| 数据结构 | 通常使用 优先队列(最小堆) 来高效选取最小边。 | 核心是使用 并查集 来高效判断和合并连通分量,避免环的形成。 |
| 时间复杂度 | 朴素实现为 O(V²),使用优先队列可优化至 O(E log V)。 | 主要开销在于边排序,为 O(E log E),近似为 O(E log V)。 |
| 适用场景 | 在边非常多的稠密图中通常表现更好。 | 在边相对较少的稀疏图中更具优势。 |
💡 了解算法理论基础与实现技巧
理解算法背后的“为什么”和具体“怎么做”,能让你更扎实地掌握它们。
贪心选择性质与安全边:两种算法都属于贪心算法,其正确性依赖于一个关键概念:每次选择的最小权值边(连接当前生成树和外部顶点对Prim而言;当前权值最小且不形成环的边对Kruskal而言)是构成最小生成树的安全边。Prim算法在实现时,通常维护一个lowcost数组来记录各顶点到当前生成树的最小距离,并不断更新它。Kruskal算法的高效性则严重依赖于并查集,用于快速判断两个顶点是否已在同一连通分量中。
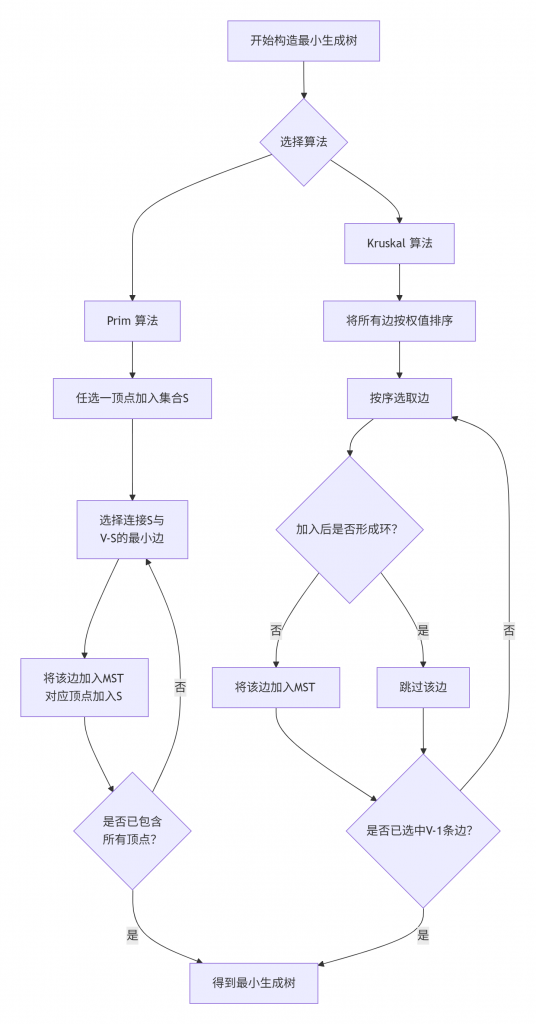
⚠️ 留意常见陷阱与进阶概念
学习时,注意一些细节和进阶知识点,能让你更好地应对复杂情况。
- 图的假设:算法默认针对的是无向、连通、带权且权值非负的图。如果图不连通,则最小生成树不存在;如果存在负权边,只要不形成负权环,算法仍然适用,但需要理解其含义。
- 关键边与伪关键边:这是一个进阶概念。关键边是指如果这条边不存在,最小生成树的总权重会增大;伪关键边则是指它出现在某个最小生成树中,但并非所有最小生成树都包含它。理解这一点有助于分析最小生成树的唯一性和稳定性。
- 其他算法:除了Prim和Kruskal,还可以了解Boruvka算法,它特别适合并行计算。
