时空复杂度

定义

算法: 解决一个实际问题的方法和具体步骤。算法是程序设计的灵魂。

程序 = 算法 + 数据结构

算法 -> 逻辑

数据结构 -> 存储，包括线性、树型、图

算法：排序、枚举、搜索、递推….

算法特征

可行性

算法中每一步运算应该是可行的。算法原则上能够精确地运行，而且人能用笔和纸做有限次运算后即可完成。

确定性

算法的每一步骤必须有确切的定义，读者理解时不会产生二义性。并且，在任何条件下，算法只有唯一的一条执行路径，对于相同的输入只能得出相同的输出。如在算法中不允许有“计算8/0”或“将7或8与x相加”之类的运算，因为前者的计算结果是什么不清楚，而后者对于两种可能的运算应做哪一种也不知道。

有穷性

一个算法应包括有限的运算步骤，执行了有穷的操作后将终止运算，不能是个死循环.

输入

一个算法有0个或多个输入，以描述运算对象的初始情况，所谓0个输入是指算法本身定义了初始条件。如在5个数中找出最小的数，则有5个输入。

输出

一个算法有一个或多个输出，以反映对输入数据加工后的结果，这是算法设计的目的。它们是同输入有着某种特定关系的量。如上述在5个数中找出最小的数，它输出为最小的数。如果一个程序没有输出，这个程序就毫无意义了

算法的基本结构

任何一个算法都可以表示成三种基本结构：顺序结构、分支结构和循环结构。

顺序结构

顺序结构是一种最简单、最基本的控制结构。计算机从前往后，依次执行所有的操作步骤，不遗漏、不重复

分支结构

分支结构由一个“判断条件”和两个“分支”构成，根据判断条件的成立与否，决定执行哪一条分支路径

循环结构

循环结构又称重复结构，目的是将某一条或某一组语句重复执行若干次，其中的“某一条或某一组语句”称为循环体。

算法的时间和空间复杂度

时间复杂度：算法运行需要的时间，一般将语句执行次数作为时间复杂度

int sum = 0;   // 运行一次
int total = 0; // 运行一次
for (int i = 0; i < n; i++)
{
    total = total + i   // 运行n次
}

T(n) = 1 + 1 + … + 1

时间复杂度用大写字母”O”表示, 只保留数量级最大的一项,并忽略系数.

所以上面的时间复杂度：O(n)

列子一个算法的计算的次数是 3N^3 + N^2 + 10^3 他的时间复杂度是O(N^3)

时间测量

#include <ctime>
#include <iostream>
using namespace std;

const int MAXN = 1e7;
int main()
{
	int sum = 0;
	
	clock_t startTime = clock();
	for(int i = 1; i <= MAXN; i++) {
		sum += i;		
	}

	clock_t endTime = clock();
	cout << double(endTime - startTime) / CLOCKS_PER_SEC << "s" << endl;
	
	return 0;
 }

常数阶 O(1)

下面这个算法，是利用高斯定理计算1， 2， ……n个数的和。

int sum = 0, n = 100; /*执行一次*/
sum = (1 + n) * n / 2; /*执行一次*/
printf("%d",sum); /*执行一次*/

线性阶 O(n)

线性阶的循环结构会复杂很多。要确定某个算法的阶次，我们常常需要确定某个特定语句或某个语句集运行的次数。因此，我们要分析算法的复杂度，关键就是要分析循环结构的运行情况。下面这段代码，它的循环的时间复杂度为O(n)，因为循环体中的代码要执行n次。

int i;
for(i = 0; i < n; i++){
/*时间复杂度为O(1)的程序步骤序列*/
}

对数阶 O(logn)

如下代码：

int count = 1;
while (count < n) {
    count = count * 2;
    /*时间复杂度为O(1)的程序步骤序列*/
}

平方阶 O(N^2)

for (int i = 0; i < n; i++) {
    for (int j = i; i < n; i++) {
        total = total + i   // 运行n次
    }
}

立方阶 O(N^3)

for (int i = 0; i < n; i++) {
    for (int j = 0; i < n; i++) {
        for (int j = 0; i < n; i++) {
            total = total + i   // 运行n次
        }
    }
}

O(2^n)

求子集

O(n!)

旅行商问题：从一个城市出发，经过所有城市后返回出发地，求最短的路径。如果用朴素算法，第一个城市有n种选择，第二个有n-1种选择，依次类推，复杂度为O(n!)。

时间复杂度关系：

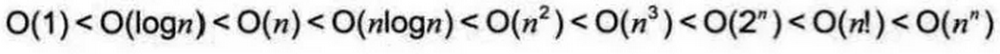
题目数据规模和时间复杂度

信息学竞赛中, 一般可以认为1s能执行10⁷次运算.

空间复杂度：算法占用空间的大小

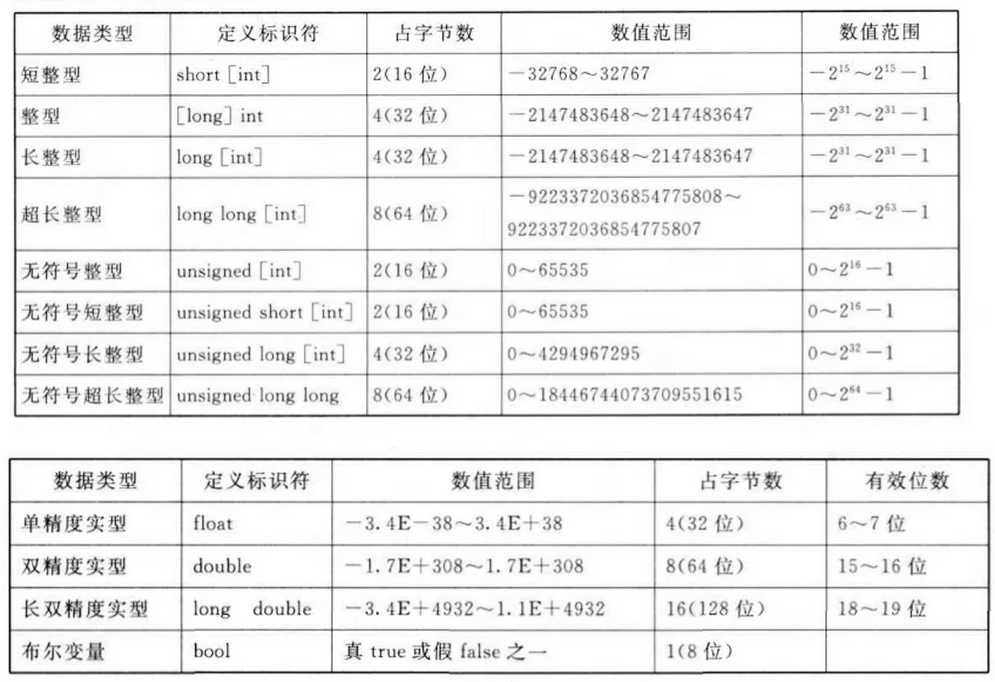
数值范围

字符型       [signed] char -128~+127
无符号字符型 unsigned char 0~255

短整型       short [int] -32768~32768
无符号短整型 unsigned short[int] 0~65535

整型         [signed]int -2147483648~+2147483647   ---  2 x 10^9
无符号整型   unsigned[int] 0~4294967295 ---  4 X 10^9

(64bit 8Bytes)
long long的最大值：9223372036854775807   ---  9 X 10^18
long long的最小值：-9223372036854775808
unsigned long long的最大值：18446744073709551616

数据规模

信息学竞赛中一般是128M或者256M的空间限制.

256M = 256 * 1024 * 1024 = 268435456字节

128M = 131072KB = 134217728字节

128M的情况下开int型变量的一维数组最多是3千万, long long型1千5百万, char型1亿左右

换成数组的最大值:

int a[3e7];
int a[5000][5000];
long long a[1e7];
long long a[4000][4000];

复杂度的威力

这是一个很著名的故事：阿基米德与国王下棋，国王输了，国王问阿基米德要什么奖赏？阿基米德对国王说：“我只要在棋盘上第一格放一粒米，第二格放二粒，第三格放四粒，第四格放十六粒…按这个方法放满整个棋盘就行．”国王以为要不了多少粮食，就随口答应了，结果国王输了．

IPv6 128bit

IPv6 128 位的地址长度可以提供 3.402823669 × 10³⁸ 个地址。

地球上一般一粒沙子的体积是0.0368立方毫米也就是3.68×10^-11立方米. 地球半径约为6400km，用球的体积公式算下来，地球体积大约是1.098×10^{12立方千米，合1.098×10}30 立方毫米。假设整个地球都是沙子，一粒沙子的大小是1立方毫米，那么地球约有1.098×10^30个沙子。

换句话说, 如果采用对数的算法, 只要128次运算就能找出地球上的那一个沙子.

典型问题：
1491 扫雷游戏
1549 铺地毯
1453 乒乓球
1550 玩具谜题