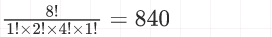一、两个基础问题
问题一:从甲、乙、丙3名同学中选出2名去参加某天一项活动,有多少种不同的选法?写出这些选法?
解析:甲、乙;甲、丙;乙、丙 一共3种
问题二:从甲、乙、丙3名同学中选出2名去参加某天的一项活动,其中1名同学参加 上午的活动,1名同学参加下午的活动,有多少种不同的选法,写出这些选法?
解析:
选甲乙去:甲、乙;乙、甲;
选甲丙去:甲、丙;丙、甲;
选乙丙去:乙、丙;丙、乙;
6种
二、加法原理 (分类计数)
完成一件事有n类办法:在第一类办法中有m1种不同的方法,在第二类办法中有m2种不同的方法,…,在第n类办法中有mn种不同的方法,那么完成这件事共有N=m1+m2+m3+…+mn种不同的方法。
三、乘法原理 (分步计数)
完成一件事需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,…,做第n步有mn种不同的方法,那么完成这件事共有N=m1*m2*m3*…*mn种不同的方法。
请判断如下问题是组合问题还是排列问题?
(a)设集合A={a,b, c, d} ,则集合A的含有3个元素的子集有多少个?组合问题
(b)某铁路线上有5个车站,则这条铁路线上共需准备多少种车票? 排列问题
(c)10名同学分成人数相同的数学和英语两个学习小组,共有多少种分法?组合问题
(d)10人聚会,见面后每两人之间要握手相互问候,共需握手多少次?组合问题
(e)从4个风景点中选出2个游览,有多少种不同的方法? 组合问题
(f)从4个风景点中选出2个,并确定这2个风景点的游览顺序,有多少种不同的方法? 排列问题
请尝试写出a,b,c这3个元素,选取2个元素的排列和组合的结果分别有哪些?
组合结果: ab , ac , be
排歹结果: ab , ac , ad , be , bd , cd 例1: 有一角、二角、五角人民币各1张,一元人民币3张,五元人民币2张, 一百元的2张,由这10张人民币可组成多少种不同的币值?
解析:
- {一角,二角,五角} 每个选 和 不选2种选择, 共种23=8种币值(包括0);
- {一元,一元,一元} 共可以组成零元、一元、两元和三元,共4种币值;
- {五元,五元} 共可以组成零元、五元和十元,共3种币值;
- {一百元,一百元} 共可以组成零元、一百元和两百元,共3种币值,
- 每个括号中币值总和不超过下一个括号的一个面值,所以有: 8*4*3*3=288种 (包括零元在内),进而可组成不同的币值的种类为: 288 – 1 = 287 种.
例2: 图中有4个编号为1、2、3、4的小三角形,要在每一个小三角形中涂上红、黄、蓝、白、黑五种颜色中的一种,使有相邻边的小三角形颜色不同,共有多少种不同的涂色方法?
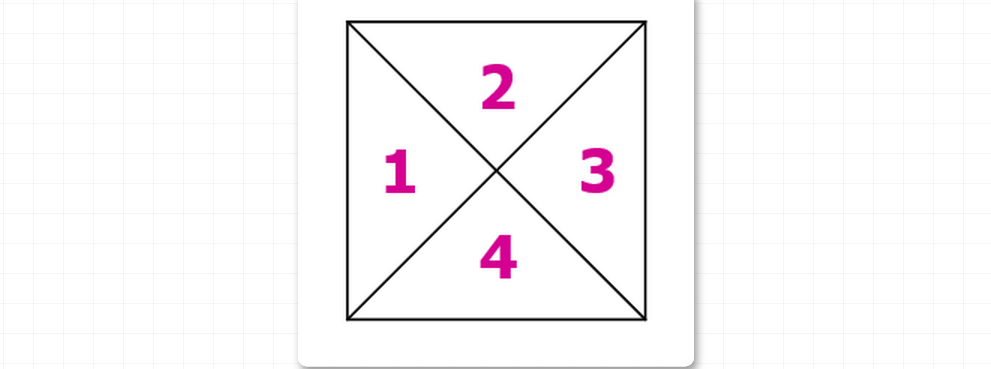
解析: 染色问题经典题
- 1号区域,有5种颜色可选,即有5种涂法,
- 若2、4号区域涂不同的颜色, 2–4种,4–3种,3-3种,一共4*3*3=36种;
- 若2、4号区域涂相同的颜色,2和4–4种,3–4种,一共有4*4=16种;
- 共有5×(36+16)=5×52=260。
四、排列组合
- 排列的定义 从n个不同元素中,任取m个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列。
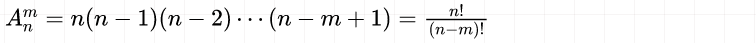
- 组合的定义 从n个不同元素中,选出m个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合。

- 常用等式
- \(C_{n}^{m}\)=\(C_{n}^{n-m}\)
理解: 从n中选m个 剩余n-m个, 和 选n-m个 剩余n个的方法相同.
2. \(C_{n}^{m}\)=\(C_{n-1}^{m}\)+\(C_{n-1}^{m-1}\)
理解:
选中的m个数中分两种情况, 包含 1 和 不包含 1.
包含1的情况: 先选取1, 然后从剩下的数 n-1 中选择 m-1 个:\(C_{n-1}^{m-1}\).
不包含1的情况: 从n中排除掉 1, 从剩下的 n-1个中选择 m个:\(C_{n-1}^{m}\).
3. \(C_{n}^{0}\) + \(C_{n}^{1}\) + \(C_{n}^{2}\) + … + \(C_{n}^{n}\) = \(2^{n}\)
理解:
左边: 是从 n 个数中, 选任意多个数的方案.
右边: n 个数中每个有2个选择, 选和不选, 方案数是2n
- 排列&组合的区别
通俗地说,组合不分顺序,而排列分顺序,也就是说,对于数列 1,2,有以下两种排列:1, 2 和 2, 1,但是仅有一种组合 1, 2.
五、排列组合解题技巧
A. 分类计数原理:做一件事情,完成它可以有n类办法,在第一类办法中有m1种不同的方法,在第二类办法中有m2种不同的方法,……,在第n类办法中有mn种不同的方法, 那么完成这件事共有m1+m2 + … + mn种不同的方法。
B. 分步计数原理:做一件事情,完成它需要分成n个步骤,做第一个步骤有m1种不同的方法,做第二个步骤有m2种不同的方法,……,做第n个步骤有mn种不同的方法, 那么完成这件事共有m1* m2 * … * mn种不同的方法。
C. 可重排列:在m个不同的元素中,每次取出n个元素,元素可以重复出现,按照一定的顺序那么第 一、第二……第n位是的选取元素的方法都是m种;所以从m个不同的元素中,每次取出n个元素的可重复的排列数为mn。
D. 解排列组合问题
- ① 要弄清一件事是“分类”还是“分步”完成;
- ② 对于元素之间的关系,还要考虑是“有序的”还是“无序的,也就是会正确使用分类计数原理和分步计数原理、排列定义和组合定义。
不相邻问题,选空插入法
例3:学校师生合影,共 8 个学生,4 个老师,要求老师在学生中间,且老师互不相邻,共有多少种不同的合影方式 ?
解析:先排学生共有A\(_{8}^{8}\)种排法, 然后把老师插入学生之间的空档,共有 7 个空档可插, 选其中的 4 个空档, 共有A\(_{7}^{4}\)种选法.根据乘法原理,共有的不同A\(_{8}^{8}\) A\(_{7}^{4}\)种.
「插入法」:对于某两个元素或者几个元素要求不相邻的问题, 可以用插入法. 即先排好没有限制条件的元素, 然后将有限制条件的元素按要求插入排好元素的空档之中即可.
相邻问题-整体捆绑法
例4:5个男生3个女生排成一排, 3个女生要排在一起, 有多少种不同的排法?
解析: 因为女生要排在一起, 所以可以将3个女生看成是一个人, 与5个男生作全排列,有A\(_{6}^{6}\) 种排法, 其中女生内部也有A\(_{3}^{3}\) 种排法,根据乘法原理, 共有 A\(_{6}^{6}\)A\(_{3}^{3}\) 种不同的排法.
「捆绑法:」 要求某几个元素必须排在一起的问题, 可以用捆绑法来解决问题. 即将需要相邻的元素合并为一个元素, 再与其它元素一起作排列, 同时要注意合并元素内部也可以作排列.
剩余法
例5:袋中有不同年份生产的5分硬币23个, 不同年份生产的1角硬币10个, 如果从袋中取出2元钱,有多少种取法?
解析:此题是一个组合问题,若是直接考虑取钱的问题的话,情况比较多,也显得比较凌乱,难以理出头绪来。但是如果根据组合数性质考虑剩余问题的话,就会很容易解决问题.
解:把所有的硬币全部取出来, 将得到 0.05×23+0.10×10=2.15元,所以比2元多0.15元, 所以剩下0.15元即剩下3个5分或1个5分与1个1角,所以共有A\(_{23}^{3}\)+A\(_{23}^{1}\)A\(_{10}^{1}\)种取法.
「剩余法:」 在组合问题中,有多少取法,就有多少种剩法, 他们是一一对应的,因此,当求取法困难时,可转化为求剩法.
对等法
例6:学校安排考试科目9门, 语文要在数学之前考, 有多少种不同的安排顺序?
解析:对于任何一个排列问题,就其中的两个元素来讲的话, 他们的排列顺序只有两种情况,并且在整个排列中, 他们出现的机会是均等的,因此要求其中的某一种情况,能够得到全体, 那么问题就可以解决了。并且也避免了问题的复杂性。
不加任何限制条件, 整个排法有A\(_{9}^{9}\)种,“语文安排在数学之前考” 与 “数学安排在语文之前考”的排法是相等的, 所以语文安排在数学之前考的排法共有 A\(_{9}^{9}\)÷2 种。
「对等法:」 在有些题目中,它的限制条件的肯定与否定是对等的,各占全体的二分之一。在求解中只要求出全体, 就可以得到所求。
排异法
例7:某个班级共有43位同学,从中任抽5人,正、副班长、团支部书记至少有一人在内的抽法有多少种?
解析: 此题若是直接去考虑的话,就要将问题分成好几种情况,这样解题的话,容易造成各种情况遗漏或者重复的情况. 而如果从此问题相反的方面去考虑的话,不但容易理解,而且在计算中也是非常的简便.这样就可以简化计算过程.
43人中任抽5人的方法有A\(_{43}^{5}\)种, 正副班长, 团支部书记都不在内的抽法有A\(_{40}^{5}\)种, 所以正副班长,团支部书记至少有1人在内的抽法有 A\(_{43}^{5}\) – A\(_{40}^{5}\) 种。
「排异法:」 有些问题, 正面直接考虑比较复杂, 而它的反面往往比较简捷,可以先求出它的反面, 再从整体中排除.
圆周排列
圆周排列与直线排列最大的区别是圆排列没有首尾之分
N个元素的圆周排列:8人围桌而坐,共有8!/8=7!种坐法
A\(_{n}^{n}\)÷n=(n-1)!
从n个不同的元素中取r个沿一圆周排列,排列的方案:
A\(_{n}^{r}\)÷n
重复元素的排列
如: n1个 a, n2个 b, n3个C, 排成一排, 有多少种排列方法?
(n1+n2+n3)!÷(n1!n2!n3!)
重复元素的组合
从n种不同元素中取r个元素的组合. 允许有重复元素的组合:

例8: 平面上有3条平行直线, 每条直线分别上有 5, 6, 7个点, 且不同直线上3个点都不在同一条直线上. 问用这些点作为顶点, 能组成多少个不同的四边形().
解析:两种情况:
4个点, 在两条直线上, A上2个点, B上2个点:
C\(_{5}^{2}\)×C\(_{6}^{2}\)=10×15=150
同理 AC上四边形个数:
C\(_{5}^{2}\)×C\(_{7}^{2}\)=10×21=210
BC上:
C\(_{5}^{2}\)×C\(_{6}^{2}\)=10×15=150
在一直线上有2点, 另外2点分别在另外两条直线上
A上2个点, BC上各1个:
C\(_{5}^{2}\)×C\(_{6}^{1}\)×C\(_{7}^{1}\)=10×6×7=420
B上2个点: AC上各1个
C\(_{6}^{2}\)×C\(_{5}^{1}\)×C\(_{7}^{1}\)=15×6×7=525
C上2个点 AB各1个
C\(_{7}^{2}\)×C\(_{5}^{1}\)×C\(_{6}^{1}\)=21×5×7=630
共有 150 + 210 + 315 + 420 + 525 + 630 = 2250.
例9: 由3个 a, 5 个 b, 2 个 c 组成的所字串中包含子串”abc”的共有多少个( )
解析: “abc”看作一个整体, 剩下了2个a, 4个b, 1个c. 一共 8个含有相同元素的全排列. 所以有: