拓扑排序 – 红栗

有向无环图 (DAG) 拓扑排序

定义如果一个有向图不存在环，也就是任意结点都无法通过一些有向边回到自身，那么称这个有向图为有向无环图。英文名叫 Directed Acyclic Graph，缩写是 DAG。

对一个有向无环图 G 进行拓扑排序，是将 G 中所有顶点排成一个线性序列，使得图中任意一对顶点 u 和 v ，若边<u,v> ∈ E(G)，则 u 在线性序列中出现在 v 之前。通常，这样的线性序列称为满足拓扑次序(Topological Order)的序列，简称拓扑序列。简单的说，由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。

性质

能拓扑排序的图，一定是有向无环图；

如果有环，那么环上的任意两个节点在任意序列中都不满足条件了。

有向无环图，一定能拓扑排序；

如何判定一个图是否是有向无环图呢？

检验它是否可以进行拓扑排序即可。

拓扑排序有何作用？

拓扑排序主要用来解决有向图中的依赖解析（dependency resolution）问题。

游戏升级的先后顺序也是一个拓扑序.

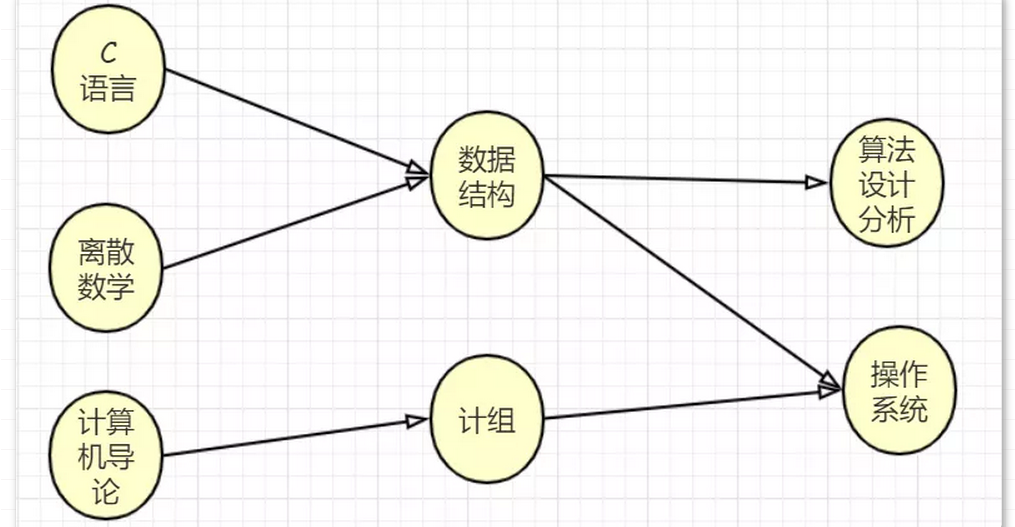
用计算机专业的几门课程的学习次序来描述拓扑关系，显然对于一门课来说，必须先学习它的先导课程才能更好地学习这门课程，比如学数据结构必须先学习C语言和离散数学，而且先导课程中不能有环，否则没有尽头了

拓扑排序的结果不唯一，比如“C语言”和“离散数学”就可以换下顺序，又或者把“计算机导论”向前放在任何一个位置都可以。总结一下就是，如果某一门课没有先导课程或是所有的先导课程都已经学习完毕，那么这门课就可以学习了。

算法描述

对于一个有向无环图

初始化一个 int[] inDegree 保存每一个结点的入度。
对于图中的每一个结点的子结点，将其子结点的入度加1。
选取入度为 0 的结点开始遍历，并将该节点加入输出。
对于遍历过的每个结点，更新其子结点的入度：将子结点的入度减1。
重复步骤3，直到遍历完所有的结点。
如果无法遍历完所有的结点，则意味着当前的图不是有向无环图。不存在拓扑排序。

解释一下，假设A为一个入度为0的结点，就表示A结点没有前驱结点，可以直接做，把A完成后，对于A的所有后继结点来说，前驱结点就完成了一个，入度进行−1。

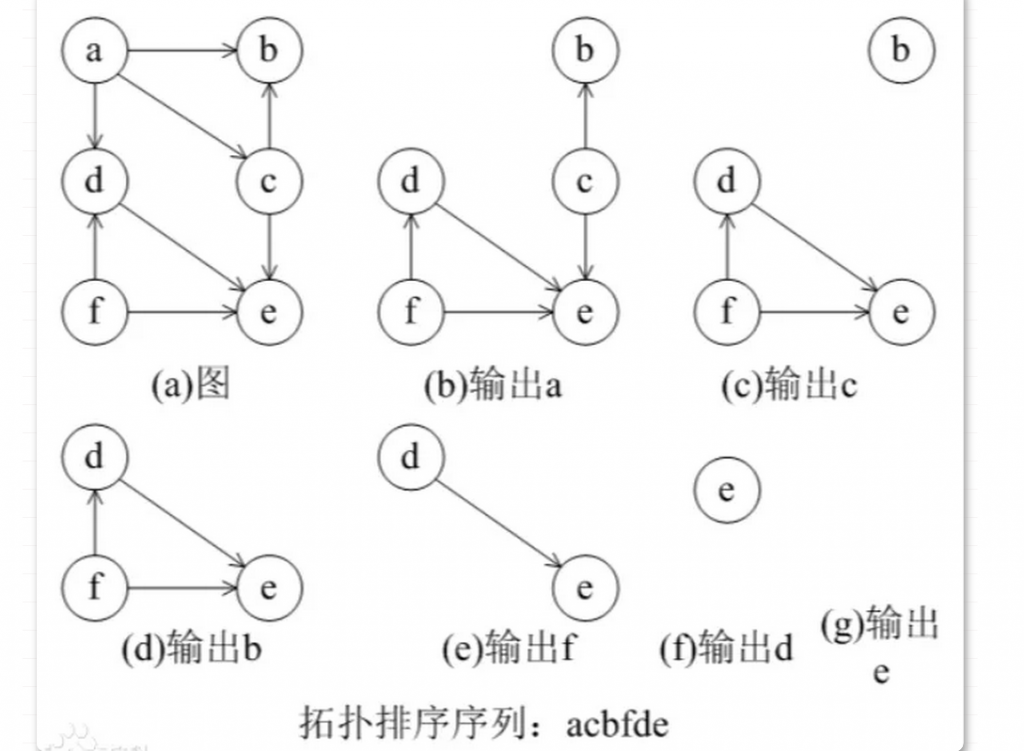
时间复杂度

如果 DAG 网络有 n 个顶点，m 条边，在拓扑排序的过程中，搜索入度为零的顶点所需的时间是 O(n)。在正常情况下，每个顶点进一次队列，出一次队列，所需时间 O(n)。每个顶点入度减 1 的运算共执行了 m 次。所以总的时间复杂为 O(n+m)。

因为拓扑排序的结果不唯一，所以题目一般会要求按某种顺序输出，就需要使用优先级队列，这里采取了最小字典序输出。

模板

void tpsort() {
    queue<int>  q;

 for (int i = 1; i <= n; i++) {
        if (!in[i]) {
            q.push(i);
        }
    }

    while (!q.empty()) {
        int u = q.front();
  q.pop();
        ans[++idx] = u;
        for (int i = hd[u]; i ; i = e[i].nxt) {
            int to = e[i].to;
   in[to]--;
            if (!in[to])
                q.push(to);
        }
    }
}

DFS 拓扑排序

#include<bits/stdc++.h>
using namespace std;

const int maxn = 1000 + 10;
const int INF = 1e9 + 7;
int T, n, m, cases;

vector<int>Map[maxn];

// 标记数组c[i] = 0 表示还未访问过点
// c[i] = 1表示已经访问过点i，并且还递归访问过它的所有子孙?
// c[i] = -1表示正在访问中，尚未返回
int c[maxn];
int topo[maxn], t;

bool dfs(int u)//从u出发
{
    c[u] = -1;//访问标志
    for(int i = 0; i < Map[u].size(); i++)
    {
        int v = Map[u][i];

     //如果子孙比父亲先访问，说明存在有向环，失败退出
      if(c[v] < 0)return false;
  else if(!c[v] && !dfs(v))
   return false;
   //如果子孙未被访问，访问子孙返回假，说明也是失败
    }

    c[u] = 1;
    topo[--t] = u;
 //在递归结束才加入topo排序中?
 // 这是由于在最深层次递归中，已经访问到了尽头，
 //此时才是拓扑排序中的最后一个元素
    return true;
}

bool tpsort()
{
    t = n;
    memset(c, 0, sizeof(c));
    for(int u = 1; u <= n; u++)if(!c[u])
        if(!dfs(u))return false;
    return true;
}
int main()
{
    while(cin >> n >> m)
    {
        if(!n && !m)break;
        int u, v;
        for(int i = 0;  i <= n; i++)Map[i].clear();
        for(int i = 0; i < m; i++)
        {
            cin >> u >> v;
            Map[u].push_back(v);
        }
        if(tpsort())
        {
            cout<<"Great! There is not cycle."<<endl;
            for(int i = 0; i < n; i++)cout<<topo[i]<<" ";
            cout<<endl;
        }
        else cout<<"Network has a cycle!"<<endl;
    }
    return 0;
}