建图

建图 – 根据题意

重点是怎么看出这是一个图论的问题, 怎么抽象出结点和边, 然后用最短路模板解决掉.

建图 – 反向建图

单源最短路径是求的源点到其他所有点的最短路.

反向建图之后, 就能求出其他所有点到源点的最短路.

建图 – 超级源点和汇点

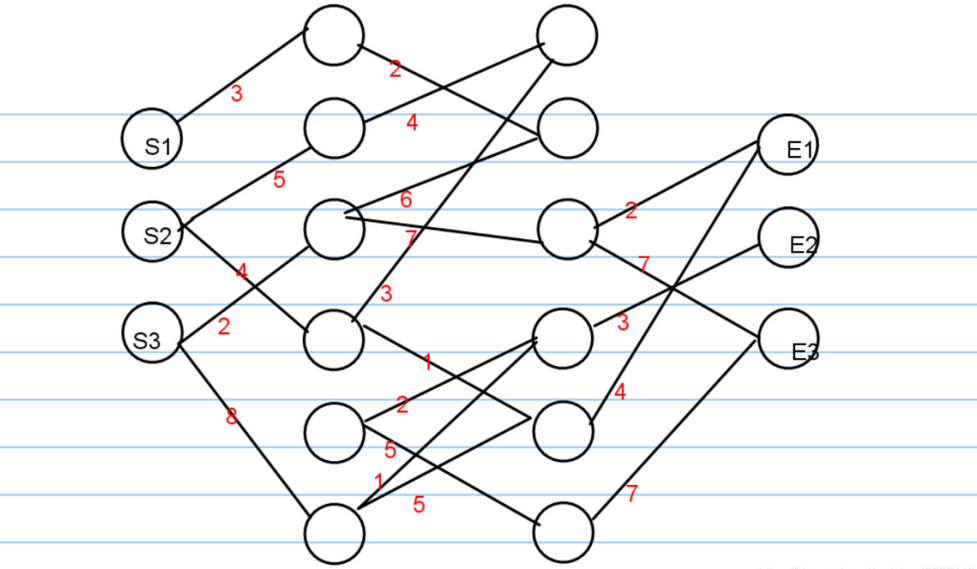
背景：给出题目，在一张图中有多个点起点，一个终点，求所有起点到终点的最短距离。

解题方法：

1. 跑N遍单源最短路，但是这样是不行的肯定超时。
2. floyd求出所有最短路，枚举每个起点到终点的距离，这个似乎比法1更慢。
3. 反向建图，反向跑一遍Dijkstra，或者SPFA，这样就能求到终点到起点的距离，在枚举最小的一个即可，时间复杂度为一遍最短路加枚举N。
4. 建立超级源点，虚拟出一个点作为源点，源点到所有起点的距离都是0，那么这样求超级源点到终点的最短距离就是所有起点到终点的距离的最短一个，时间复杂度为一遍最短路。

题目二：给出一张图中有一个起点，有多个终点，求一个起点到所有终点的最短距离。

解题方法：

1. 直接忽略floyd
2. 一遍最短路（SPFA或Dijkstra），枚举 N。
3. 建立超级汇点，所有终点到汇点的距离为0，一遍最短路即可出答案。

题目三: 给出一张图，图中有若干起点与若干终点，在所有终点到起点的距离中的最短距离。

解题方法:

1. 跑若干遍最短路，找到所有最短距离，比较得出最小值
2. 建立超级源点，建立超级汇点，一遍Dijkstra或SPFA即可。

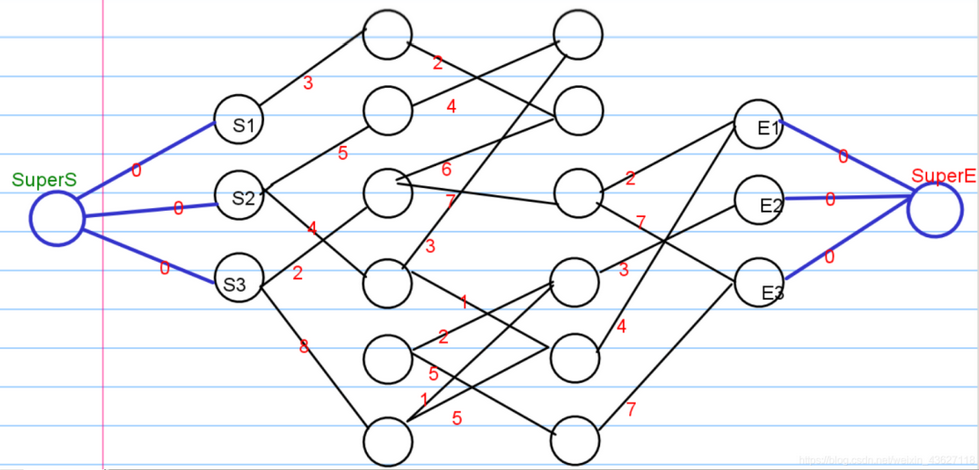
通过上面我们大致知道超级源点超级汇点的建立的条件，而且通过超级源点（汇点）可以极大的减少题目的时间复杂度.