一、并查集是什么
并查集 是一种树型的数据结构,用于处理一些不相交集合的合并及査询问题。
并查集的思想是用一个数组表示了整片森林(parent),树的根节点唯一标识了一个集合,我们只要找到了某个元素的的树根,就能确定它在哪个集合里。
并查集一般处理的问题:
(1)合并:将若干点合并到一个或多个集合(构成一棵树或多棵树),将多个集合合并 (多棵树合并为一颗树);
(2)査询:询问某2个点是否在同一个集合中(查询);
(3)其他:计算一共有几个集合(几棵树)。
并查集的实现方法
(1)举例说明:假设有如下8个点:1 2 3 4 5 6 7 8, 假设如下两两的结点在一个集合中,通过并查 集构建过程的模拟来看最终有几个集合,并理解并查集的构建过程和查询过程。 两两在一个集合中的结点有:
1 3
1 2
5 4
2 4
6 8
8 7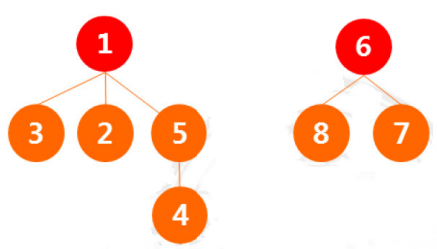
(2)数据结构的实现 实际操作时,我们会使用一个点来代表整个集合,即一个元素的根结点(可以理解为父 亲)。
实现方法
我们建立一个数组fa□表示…个并查集,fa[i]表示i的父节点。
(1) 初始化:每一个点都是一个集合,因此自己的父节点就是自己fa[i]=i。
(2) 查询:每一个节点不断寻找自己的父节点,若此时自己的父节点就是自己,那么 该点为集合的根结点,返回该点。
(3) 合并:合并两个集合只需要合并两个集合的根结点,即fa[ROotA]=RootB,其中 RootA, RootB是两个元素的根结点。
(4)路径压缩:大多数情况下,在查询过程中只关心根结点是什么,并不关心这棵树的形态。因此我们可以在查询操作的时候将访问过的每个点都指向树根,这样的方法叫做路径压缩。
for(int i=l;i<=n;i++) fa[i]=i; //初始化模板
int find(int x){ //基本查询模板:求x的根
return fa[x] == x?x:find(fa[x]);
}
int find(int x){ //路径压缩查询模板
if (fa[x] != x){ //如果不是根结点
int fx = fa[x];
fa[x] = find(fa[x]); //路径压缩
value[x] += value[fx]; //父结点权值更新
}
return fa[x];
}
void merge(int x, int y){ //合并模板,x和y结点到一个集合
int px = find(x);
int py = find(y);
if (px != py){ //不在同一个集合
fa[px] = py;
}
}二、种类并查集 普通的并査集维护的是具有连通性、传递性的关系,例如亲戚的亲戚是亲戚。种类并查集是在此基础上再进行一些“分类”,类似“敌人的敌人是朋友”的分类。
1、种类并査集常规思路:扩大并査集规模。比如:要维护朋友和敌人这两个关系,则将普通并査集的规模扩大两倍,原来的1~n 还是存放朋友关系,但是n+1~2n则是存放敌人关系,然后每次操作都分别维护。
2、种类并査集加强版:上面举的例子是针对两种对立关系,但是有些题目会涉及三种循环关系,怎么做呢?其实就是将扩大两倍规模变为扩大三倍规模。
以“团队数量”题目为例,题目的两种关系已经说得很明确了,我们将朋友关系的两个人合并。对于是敌人关系 两个人,由于敌人的敌人是我的朋友,所以我们可以建立一个自己虚拟的敌人(比如:认为 x和x+n是敌人,那么如果x和y是敌人的话,y和x+n就是朋友)再与对方形成朋友关系。
三、带权并查集 带权并查集是结点存有权值信息的并查集。
相比于一般的并查集,带权并查集需要开辟两个数组:一个是f[N]用来判断集合关系;一个是value[N], 用来描述其与根节点的关系。
当两个元素之间的关系可以量化,并且关系可以合并时,可以使用带权并查集来维护元 素之间的关系。
带权并查集每个元素的权值通常描述其与并查集中祖先的关系,这种关系如何合并,路径压缩时就如何压缩
基于路径压缩,带权并查集:它的每一条边都记录了每个节点到根节点的一个权值,这个权值该设为什么由具体的问 题而定,一般都是两个节点之间的某-种相对的关系,但是考虑到权值就会有两个问题:
(1)每个节点都记录的是与根节点之间的权值,那么在find的路径压缩过程中,权值也 应该做相应的更新,因为在路径压缩之前,每个节点都是与其父节点链接着,value自然也 是与其父节点之间的权值;
(2)在两个并查集做合并的时候,权值也要做相应的更新,因为两个并查集的根节点不同。
int find(int x) {
if(f[x] == x) return x;
else{ //更新路径的值
int t = fa[x]; //记录当前父节点的编号
f[x] = find(f[x]); //路径压缩
dis[x] = dis[x] + dis[t]; //回溯时,更新权值
return f[x];
}可以看到更新权值只多了两行代码,先记录下原本父节点的编号,因为在路径压缩后父 节点就变为根节点了,再将当前节点的权值加上原本父节点的权值,此时父节点的权值已经 是父节点到根节点的权值了,因此加上这个权值就会得到当前节点到根节点的权值。
四、并查集的应用—最小生成树
在含有n个顶点的连通网中选择n-1条边,构成一棵极小连通子图,并使该连通子图中 n-1条边上权值之和达到最小,则称其为连通网的最小生成树。例如,对于如右图所示的连 通网可以有多棵权值总和不相同的生成树。
应用场景:
例如:要在n个城市之间建设道路,主要目标是要使这n个城市的任意两个之间都可 以通行,但建设道路的费用很高,且各个城市之间建设道路的费用不同,因此另一个目标是 要使建设道路的总费用最低。这就需要找到带权的最小生成树。
Kruskal 算法
基本思想:按照权值从小到大的顺序选择n-1条边,并保证这n-1条边不构成回路。 具体做法:首先构造一个只含n个顶点的森林,然后依权值从小到大从连通网中选择边 加入到森林中,并使森林中不产生回路,直至森林变成一棵树为止。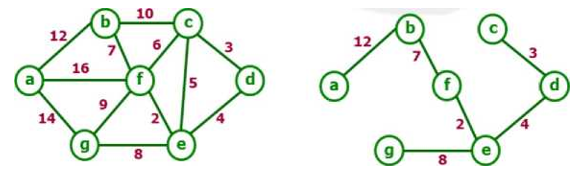
🔍 并查集核心知识要点
| 知识模块 | 关键知识点 | 说明与要点 |
|---|---|---|
| 核心概念 | 数据结构本质 | 用于管理不相交集合的树型结构,高效处理合并与查询问题。 |
| 基本操作 | 1. 查找:确定元素所属的集合(找到根节点)。 2. 合并:将两个集合合并为一个。 | |
| 表示与存储 | 父指针数组/字典 | 通常使用数组或字典,其中 fa[i] 表示元素 i 的父节点。根节点的父节点指向自己。 |
| 关键优化 | 路径压缩 | 查找时,将路径上所有节点的父节点直接指向根节点,摊平树结构。这是并查集高效的关键。 |
| 按秩合并 | 合并时,将秩较小的树合并到秩较大的树下,避免树退化成链表。秩可理解为树高度的上界。 | |
| 性能分析 | 时间复杂度 | 未经优化:查找O(n),合并O(n)。经路径压缩与按秩合并优化后,每次操作平均时间接近常数O(α(n))。 |
| 典型应用场景 | 连通性问题 | 判断图中节点是否连通、求连通分量数量。 |
| 动态连通性 | 在动态添加边的过程中实时判断连通性(如Kruskal算法求最小生成树)。 | |
| 分组与分类 | 将元素按规则分组。 | |
| 代码实现 | 模板与变种 | 1. 朴素并查集:基本操作。 2. 维护集合大小的并查集:按大小合并。 3. 带权并查集:在边上维护额外信息(如距离)。 |
| 常见陷阱 | 初始化 | 务必确保每个元素的父节点初始化为自身。 |
| 优化协同 | 路径压缩可能改变树的高度,若严格定义“秩”,路径压缩时不修改秩,二者可协同工作。 |
💡 建议你按照以下顺序亲手实现代码,深刻理解每一步的用意:
- 第一版:朴素实现。只使用父指针数组,完成基础的
find和union操作。此时,树很容易退化成链,性能最差。 - 第二版:加入路径压缩。在
find函数中增加递归的路径压缩操作。你会立即感受到查询效率的飞跃。 - 第三版:加入按秩合并。增加一个秩数组,在
union操作中比较秩的大小来决定合并顺序。这能保证树结构的平衡,将性能优化到理论极限。
⚠️ 注意常见误区
- 忘记初始化:这是最常见的错误。务必记住,在开始时每个元素都是独立的集合。
- 误解秩的含义:在路径压缩后,树的“高度”可能变化,但按秩合并中的“秩”是高度的上界,并非实时高度。因此,在路径压缩时我们不需要更新秩。
- 认为优化是必须的:对于小规模数据或简单问题,朴素的并查集可能就足够了。但理解优化是为了在面临大规模、高性能需求时,你有工具可以应对。
并查集是处理分组和连通性问题的利器,核心在于理解其树形结构与高效的路径压缩、按秩合并优化策略。希望这份梳理能帮助你扎实地掌握这个重要的数据结构。
