一、集合的运算
并:∪
交:∩
补:^ 或 ~
差: –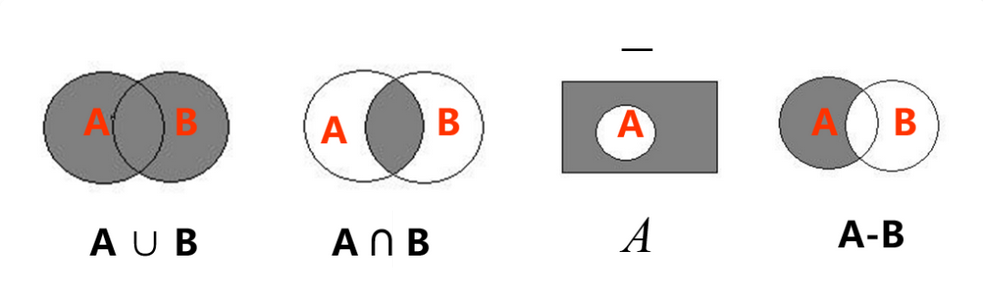
例1: 设全集 E = {1,2,3,4,5},集合 A = {1,4},B ={1,2,5},C = {2,4},则集合 (A∩B)∪C 为( )。
A 空集
B {1}
C {2,4}
D {1,5}
E {1,2,4}
答案: E
二、容斥原理
容斥原理是在计数时,必须确保没有重复,没有遗漏,使重叠部分不被重复计算。这种方法的基本思想是:
1、先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来。
2、然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理。
对有限集合S,用|S|表示S的元素个数。
A. 被计数的事物有A、B两类,那么,A类和B类元素个数总和:|A ∪ B| = |A| + |B| – |A ∩ B|
B. 如果被计数的事物有A、B、C三类,那么,A类和B类和C类元素个数总和 = A类元素个数+ B类元素个数+C类元素个数-既是A类又是B类的元素个数-既是A类又是C类的元素个数-既是B类又是C类的元素个数+既是A类又是B类而且是C类的元素个数。
|A∪B∪C| = |A|+|B|+|C| – |A ∩ B| – |B ∩ C| – |C ∩ A| + |A ∩ B ∩ C|。
例2: 2019 CSP-S-10. —次期末考试,某班有15人数学得满分,有12人语文得满分,并且有4 人语、数都是满分,那么这个班至少有一门得满分的同学有多少人?()。
A. 23
B. 21
C. 20
D. 22
解析:集合的并。被计数的事物有语、数得满分两类,“数学得满分”称为“A类元素”,“语文得满分” 称为“B类元素”,“语、数都是满分”称为“既是A类又是B类的元素”,“至少有一门得满 分的同学”称为“A类和B类元素个数”的总和。即 12 + 15 – 4 = 23.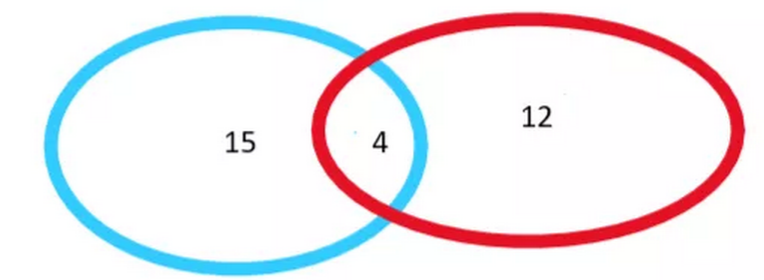
例3:10000以内,与10000互质的正整数有( )个。
A.2000
B. 4000
C. 6000
D. 8000
解析:互质的意思,与10000没有公约数,即不能被10000的质因子整除。
10000 分解质因子:10000=2*2*2*2*5*5*5*5
10000以内被2整除的数有5000个。
10000以内被5整除的数有2000个。
两者存在重复计算的数,即被10整除的数,有1000个。
被 2 或 5 整除的数有:5000 +2000 – 1000 =6000
互质的数有:10000 – 6000 = 4000个。
