能快速访问：图的存储，能让程序很快定位结点u和v的边(u, v) 。
边集数组：简单、空间使用最少；无法快递定位
邻接矩阵：简单、空间使用最大；定位最快
邻接表：空间很少，定位较快
链式前向星：空间更少，定位较快
1、邻接矩阵(数组)表示法
邻接数组表示法是以一个n*n的数组来表示一个具有n个顶点的图形。我们以数组的索引(下标)值来表示顶点,以数组的内容之来表示顶点间边是否存在(1表示存在，0表示不存在)。
根据上述无向图得到邻接矩阵，可以得出如下结论:
结论 1: 无向图的邻接矩阵是对称的
结论 2: 顶点 i 的度=第 i 行(列)中 1 的个数
注意:完全图的邻接矩阵中，对角元素为 0，其余全 1。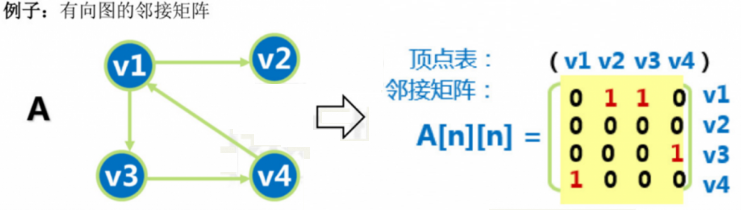
根据上述有向图得到邻接矩阵，可以得出如下结论:
结论 1: 有向图的邻接矩阵可能是不对称的
结论 2: 顶点的出度=第 i 行元素之和；顶点的入度=第 i 列元素之和；图的度=矩阵中 1 的个数*2。
结论 3: 图的存储空间占用量只与它的顶点数有关,与边数无关:适用于边稠密的图。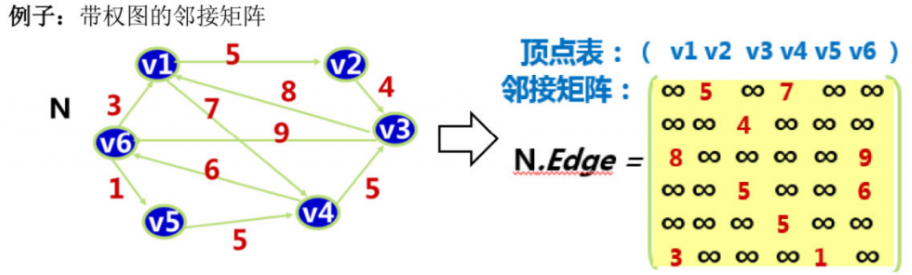
邻接矩阵法优点: 容易实现图的操作，如:求某顶点的度、判断顶点之间是否有边(弧)、找顶点的邻接点等等。
邻接矩阵法缺点: n个顶点需要n*n个单元存储边(弧)。对稀疏图而言尤其浪费空间。
2、邻接（链式）表表示法
邻接链表法：以链表来记录每个顶点的邻接顶点。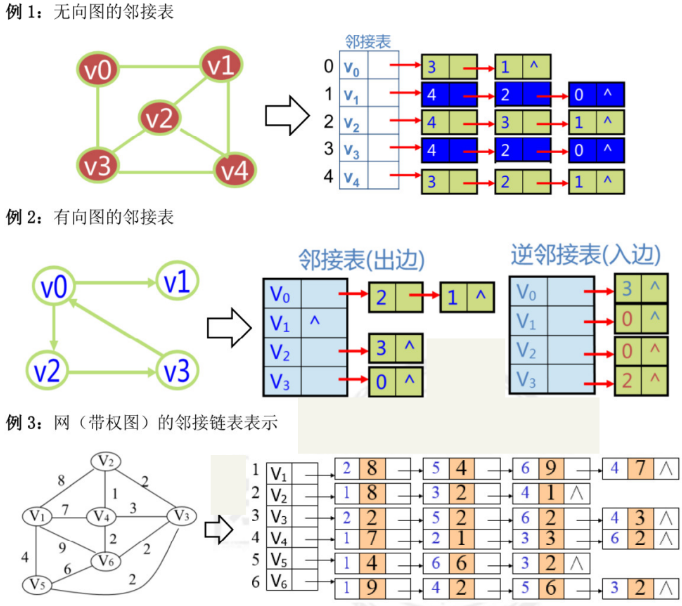
常见的做法是使用数据模拟链表、下标模拟指针来实现邻接表（代码模板）。在与链表相关的诸多结构中，邻接表是相当重要的一个。
它是树与图结构的一般化存储方式，还能用于实现散列 Hash 表。
在这样的结构中存储的数据被分成若干类，每一类的数据构成一个链表。每一类还有一个代表元素，称为该类对应链表的“表头”。所有“表头”构成一个表头数组，作为一个可以随机访问的索引，从而可以通过表头数据调位到某一类数据对应的链表。
为了方便起见，我们将这类结构统称为“邻接表”结构。