哈夫曼编码 1951年,哈夫曼在麻省理工学院(MIT)攻读博士学位,他和修读信息论课程的同学得选择是完成学期报告还是期末考试。导师罗伯特·法诺(Robert Fano)出的学期报告题目是:查找最有效的二进制编码。1952年,哈夫曼发表论文《一种构建极小多余编码的方法》(A Method for the Construction of Minimum-Redundancy Codes)中发表了这个编码方法。
在数据通信中,需要将传送的文字转换成二进制的字符串,用0,1码的不同排列来表示字符。例如,需传送的报文为 “Farris is not a Ferris wheel” ,这里用到的字符集为“f a r i s n o t e”,各字母出现的次数为{2,2,4,3,3,1, 1, 1, 1}。现要求为这些字母设计编码。要区分这些字母,如何编码才能让编码后长度最短吗?
| 字符 | 频率 | 编码 |
|---|---|---|
| i | 3 | 00 |
| s | 3 | 01 |
| f | 2 | 110 |
| a | 2 | 111 |
| n | 1 | 1000 |
| o | 1 | 1001 |
| t | 1 | 0110 |
| e | 1 | 1011 |
前缀编码 是指对字符集进行编码时,要求字符集中任一字符的编码都不是其它字符的编码的前缀。
例如:设有abcd需要编码表示(其中,a=0、b=10、c=110、d=11,则表示110的前缀可以是c或者da,不唯一).
二叉树:约定左分支表示字符‘0’,右分支表示字符‘1’,则可以用从根结点到叶子结点的路径上的分支字符串作为该叶子结点字符的编码。如此得到的编码必是前缀编码。
用构造哈夫曼树的过程生成的二进制前缀编码。哈夫曼树是一类带权路径长度最短的树。
哈夫曼树 Huffman Tree,中文名是哈夫曼树或霍夫曼树,它是最优二叉树。
给定 N 个权值作为 N 个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
路径:在一棵树中,一个结点到另一个结点之间的通路,称为路径. 例如从根结点 14 到字母 f 有条路径 14->8->4->f.
路径长度:在一条路径中,每经过一个结点,路径长度都要加 1. 从根结点到结点 f 长度为 3.
结点的权:给每一个结点赋予一个新的数值,被称为这个结点的权。结点 f 的权 就是字符 f出现的频率
结点的带权路径长度:指的是从根结点到该结点之间的路径长度与该结点的权的乘积。例如从根结点 14 到字母 f 的带权路径长度为: 3 * 2 = 6.
树的带权路径长度为树中所有叶子结点的带权路径长度之和。通常记作 “WPL” 。上图中的树的带权路径长度为:WPL = 2 * 3 + 2 * 3 + 1 * 4 + 1 * 4 + 1 * 4 + 1 * 4 + 3 * 2 + 3 * 2 = 40
构造 对于给定的有各自权值的 n 个结点,构建哈夫曼树有一个行之有效的办法:
- 在 n 个权值中选出两个最小的权值,对应的两个结点组成一个新的二叉树,且新二叉树的根结点的权值为左右孩子权值的和;
- 在原有的 n 个权值中删除那两个最小的权值,同时将新的权值加入到 n–2 个权值的行列中,以此类推;
- 重复 1 和 2 ,直到所以的结点构建成了一棵二叉树为止,这棵树就是哈夫曼树.
构造示例:




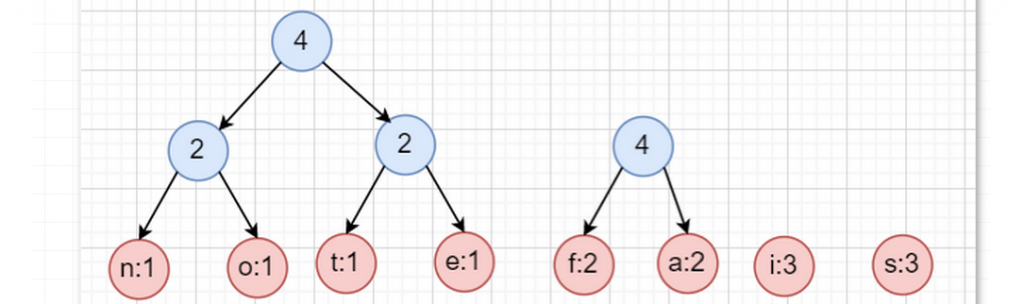
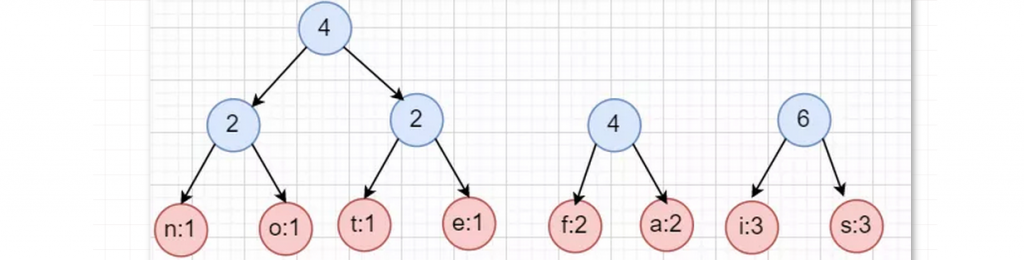


K叉哈夫曼树
K叉哈夫曼树的做法与二叉哈夫曼树相类似,只不过每次弹出的数为K个。最关键的问题在于,当k大于2时,按照这个步骤做下去可能到最后剩下的元素少于k个,可以增加(k – 1) – (n – 1) % (k – 1)个权值为0的叶子节点作虚拟点。
为什么必须要保证最后剩下的元素恰好是k个呢?假如最后的元素少于k个,那么我们完全可以前面已经加入的数随便拉一个过来补上,此时这个点的权值不变但距离变小,自然最后的结果会更小。
