计算机中带符号数的表示

一、机器数：一个数在计算机中的二进制表示形式，叫做这个数的机器数。机器数是带符号的，在计算机用一个数的最高位存放符号，正数为0，负数为1。
比如：十进制的数+3，如果计算机的字长为8位，转换成二进制就是00000011，如果是-3，就是10000011，那么这里的00000011和10000011就是机器数。
真值：因为第一位是符号位，所以机器数的形式值就不等于真正的数值。例如上面有符号数10000011，其4最高位1代表负，其真正数值是-3，而不是形式值131（10000011转换成十进制等于131）。所以，为区别起见，将带符号位的机器数对应的真正数值称为机器数的真值。
例：00000001的真值为+1，10000001的真值为-1。

二、原码、反码、补码 原码、反码、补码是计算机存储一个具体数字的编码方式。数值在计算机中是以补码的方式存储的。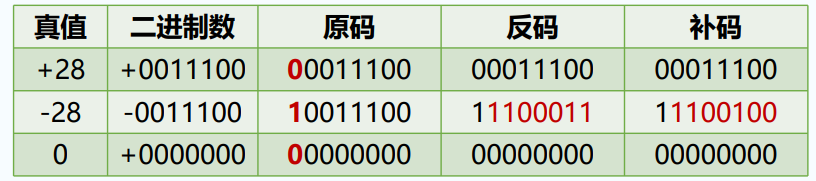原码：是最简单的机器数表示法。用最高位表示符号位. ‘1’表示负号，‘0’表示正号. 其他位存放该数的二进制的绝对值。
反码：正数的反码还是等于原码；负数的反码就是他的原码除符号位外，按位取反。
补码：正数的补码等于他的原码；负数的补码等于反码+1

32位补码表示	unsigned int	int
000000…000000	0	0
011111…111111	2147483647	2147483647
100000…000000	2147483648	-2147483648
111111…111111	4294967295	-1

可以发现，在补码下每个数值都有唯一的表示方式，并且任意两个数值做加减法运算，都等价于在32位补码下做最高位不进位的二进制加减法运算。发生算术溢出时，32位无符号整数相当于自动对2³²取模。这也解释了“有符号整数”算术上溢时出现负数的现象。

补码也被称为“二补数”，反码也叫“一补数”。

形式	加数	加数	和
32位补码	111…111	000…001	(1)000.000
int	-1	1	0
unsigned int	4294967295	1	0(mod 2³²)

32位补码	011…111	000…001	100…000
int	2147483647	1	-2147483648
unsigned int	2147483647	1	2147483648

因为用二进制表示一个int需要写出32位，比较繁琐，而用十进制表示，又不容易明显体现出补码的每一位，所以在程序设计中，常用十六进制来表示一个常数，这样只需要书写8个字符，每个字符（0~9 ,A-F）代码补码下的4个二进制位。C++的十六进制常数以“0x”开头，“0x”本身只是声明了进制，“0x”后面的部分对应具体的十六进制数值。

32位补码	int（十进制）	int（十六进制）
000000…000000	0	0x0
011111…111111	2147483647	0x7F FF FF FF
00111111 重复4次	1061109567	0x3F 3F 3F 3F
111111…111111	-1	0xFF FF FF FF

上表中的 0x3F 3F 3F 3F 是一个很有用的数值，它是满足一下两个条件的最大整数：
1. 整数的两倍不超过0x7F FF FF FF，即 int 能表示的最大正整数。
2. 整数的每8位（每个字节）都是相同的。
综上所述，0x7F 7F 7F 7F是用 memset(a,0x7f,sizeof(a)) 语句能初始化出的最大值。不过，当需要把一个数组中的数值初始化为正无穷时，为了避免加法算术上溢或者繁琐的判断，我们经常用 memset(a,0x3f,sizeof(a)) 给数组赋予 0x3F 3F 3F 3F 的值来代替。该语句在后续的学习章节中会多次出现。

三、计算机中定点数和浮点数表示 小数点在计算机中通常有两种表示方法：
1、一种是约定所有数值数据的小数点隐含在某一个固定位置上，称为定点表示法，简称定点数。
2、计算机中使用浮点数表示小数类似于以前数学中用科学计数法表示较大的数。定点数的小数点是固定的,浮点则是不固定的。因此定点数的表示范围是固定的,而浮点数的范围是可以浮动的。
例如：178.125 转化为二进制为 10110010.001，又可表示为：1.0110010001 乘以 2 的 111 次方（ 111是7的二进制表示）。
10110010001 这部分被称作尾数(M)，111 这部分被称作阶码（P），正负被称作数符（S）: 0表示正数， 1表示负数。
那么一个浮点数N可以使用三部分表示：数符（S）,阶码（P）,尾数（M）: N = 2^P * M 。
例： (178.125)₁₀=(10110010.001)₂=1.0110010001*2¹¹¹