先回顾单调队列的概念，它有以下特征：
（1）单调队列用双端队列实现，队头和队尾都能插入和弹出。手写双端队列很简单。
（2）单调队列内的元素具有单调性，从小到大，或者从大到小。
（3）单调队列的维护：每个新元素都能进入队列，它从队尾进入队列时，为维护队列的单调性，应该与队尾比较，把破坏单调性的队尾弹出。例如一个从小到大的单调队列，如果要进队的新元素a比原队尾v小，那么把v弹走，然后a继续与新的队尾比较，直到a比队尾大为止，最后a进队尾。
单调队列在DP优化中的基本应用，是对这样一类DP方程进行优化：
dp[i]=min{dp[j]+a[i]+b[j]} LL(i)≤j≤R(i) –方程(1)
公式中的min也可以是max。方程的特点是其中关于 i 的项a[i]和关于 j 的项b[j]是独立的。j 被限制在窗口[L(i),R(i)]内，常见的例如给定一个窗口值 k ，i−k≤j≤i。这个DP方程的编程实现，如果简单地对 i 做外层循环，对 j 做内层循环，复杂度O(n2 )。如果用单调队列优化，复杂度可优化到 O(n)。
为什么单调队列能优化这个DP方程？
概况地说， 单调队列优化算法能把内外 i、j 两层循环，精简到一层循环。其本质原因是“外层i 变化时，不同的 i 所对应的内层j 的窗口有重叠”。如下图所示，i=i1 时，对应的j1 的移动窗口（窗口内处理DP决策）范围是上面的阴影部分；i=i2 时，对应的j2 处理的移动窗口范围是下面的阴影；两部分有重叠。当i 从i1 增加到i2 时，这些重叠的部分被重复计算，如果减少这些重复，就得到了优化。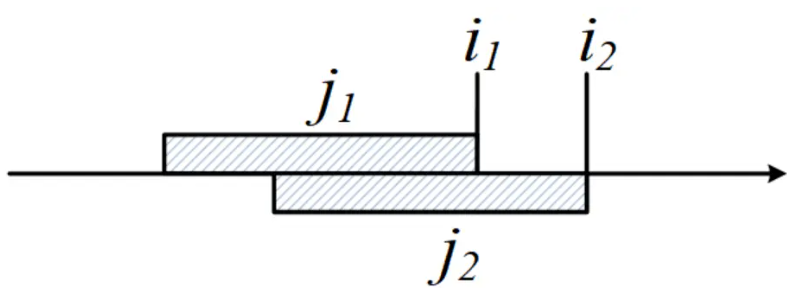
图 外层i和内层j的循环
在窗口内处理的这些决策，有两种情况：
① 被排除的不合格决策。内层循环 j 排除的不合格决策，在外层循环 i 增大时，需要重复排除。
② 未被排除的决策。内层 j 未排除的决策，在外层 i 增大时，仍然能按原来的顺序被用到。
那么可以用单调队列统一处理这些决策，从而精简到只用一个循环，得到优化。下面详细介绍单调队列的操作。
① 求一个dp[i]。i 是外层循环，j 是内层循环，在做j的内层循环时，可以把外层的 i 看成一个定值。此时a[i]可以看成常量，把j看成窗口[L(i), R(i)]内的变量，DP方程(1)等价于：
dp[i]=min{dp[j]+b[j]}+a[i]
问题转化为求窗口[L(i),R(i)]内的最优值min{dp[j]+b[j]}。记ds[j]=dp[j]+b[j],在窗口内，用单调队列处理ds[j]，排除掉不合格的决策，最后求得区间内的最优值，最优值即队首。得到窗口内的最优值后，就可以求得dp[i]。另外，队列中留下的决策，在i 变化后仍然有用。请注意，队列处理的决策 ds[j] 只和 j 有关，和 i 无关，这是本优化方法的关键。如果既和 i 有关，又和j 有关，它就不能在下一步“（2）求所有的dp[i]”时得到应用。具体来说是这样的：1）如果ds[j]只和j 有关，那么一个较小的 i1 操作的某个策略ds[j]，和一个较大的 i2 所操作的某个策略ds[j]是相等的，从而产生了重复性，可以优化；2）如果ds[]和i 、j 都有关，那么就没有重复性，无法优化。请结合后面的例题深入理解。
② 求所有的dp[i]。考虑外层循环i变化时的优化方法。一个较小的i 1 所排除的ds[j]，在处理一个较大的 i2 时，也会被排除，重复排除其实没有必要；一个较小的 i1 所得到的决策，仍能用于一个较大的 i2 。统一用一个单调队列处理所有的i ，每个ds[j]（提示：此时j 不再局限于窗口[L(i),R(i)]，而是整个区间1≤j≤n，那么ds[j]实际上就是ds[i]了)都进入队列一次，并且只进入队列一次，总复杂度O(n)。此时内外层循环i 、j 精简为一个循环i 。