区间DP

区间dp就是在区间上进行动态规划，求解一段区间上的最优解。主要是通过合并小区间的最优解，进而得出整个大区间上最优解的dp算法。

核心思想 求在一个区间上的最优解，那么可以把这个区间分割成一个个小区间，求解每个小区间的最优解，再合并小区间得到大区间即可。所以在代码实现上，我可以枚举区间长度len为每次分割成的小区间长度（由短到长不断合并），内层枚举该长度下可以的起点，自然终点也就明了了。然后在这个起点终点之间枚举分割点，求解这段小区间在某个分割点下的最优解。

问题 给定长为n的序列a[i]，每次可以将连续一段回文序列消去，消去后左右两边会接到一起，求最少消几次能消完整个序列，n≤500。

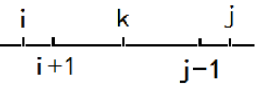
f[i][j]表示消去区间[i,j]需要的最少次数。则f[i][j]=min{f[i][k]+f[k+1][j] | i≤k<j}；

若a[i]=a[j]，则还有f[i][j]=min{f[i][k]+f[i+1][j-1] } 。   

• 这里实际上是以区间长度为阶段的，这种DP我们通常称为区间DP。
• 区间DP的做法较为固定，即枚举区间长度，再枚举左端点，之后枚举区间的断点进行转移。
• 区间类型动态规划是线性动态规划的拓展，它在分阶段划分问题时，与阶段中元素出现的顺序和由前一阶段的哪些元素合并而来有很大的关系。（例：f[i][j]=f[i][k]+f[k+1][j]）
• 区间类动态规划的特点：
  • 合并：即将两个或多个部分进行整合。
  • 特征：能将问题分解成为两两合并的形式。
  • 求解：对整个问题设最优值，枚举合并点，将问题分解成为左右两个部分，最后将左右两个部分的最优值进行合并得到原问题的最优值。
• 区间类型动态规划的典型应用有石子合并、能量项链、凸多边形的划分等。

for(int len = 1;len<=n;len++){       //枚举长度
    for(int j = 1;j+len<=n+1;j++){   //枚举起点，ends<=n
        int ends = j+len - 1;
        for(int i = j;i<ends;i++){//枚举分割点，更新小区间最优解
            dp[j][ends] = min(dp[j][ends],dp[j][i]+dp[i+1][ends]+something);
        }
    }
}