点连通度与边连通度 定义：
•在一个无向连通图中，如果有一个顶点集合V，删除顶点集合V以及与V中顶点相连（至少有一端在V中）的所有边后，原图不连通，就称这个点集V为割点集合。
•一个图的点连通度的定义为：最小割点集合中的顶点数。
•如果有一个边集合，删除这个边集合以后，原图不连通，就称这个点集为割边集合。
•一个图的边连通度的定义为：最小割边集合中的边数。
双连通图、割点与桥：
•如果一个无向连通图的点连通度大于1，则称该图是点双连通的(point biconnected)，简称双连通或重连通（即删去任意一点原图仍然连通）。一个图有割点，当且仅当这个图的点连通度为1，则割点集合的唯一元素被称为割点(cut point)（即删去割点原图不连通）。一个图可能有多个割点。
•有割点的图不一定有割边，如：
•（此时只能把顶点3删去，使得原图不连通，所以顶点3为这个图的割点。但是删去图中的任意一条边，原图仍能保持连通，所以原图无割边）
•如果一个无向连通图的边连通度大于1，则称该图是边双连通的(edge biconnected)，简称双连通或重连通。（即删去任意一边原图仍然连通）一个图有桥，当且仅当这个图的边连通度为1，则割边集合的唯一元素被称为桥(bridge)（即删去桥原图不连通）。一个图可能有多个桥。
•有割边的图也不一定有割点,如：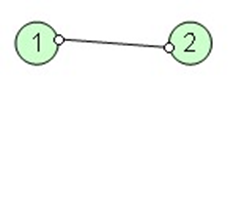
•（此时只能把边（1,2）删去，使得原图不连通，所以边（1,2）为这个图的割边。但是删去顶点1或2时，原图只剩下一个顶点，仍然为连通图，所以原图无割点）
•根据定义猜想：两个割点之间的边是否一定是割边?割边的两个端点是否一定是割点？
•两个猜想都是错误的！反例如图：（图中红色为图的割点或桥）
双连通分量：
•可以看出，点双连通与边双连通都可以简称为双连通，它们之间是有着某种联系的，下文中提到的双连通，均既可指点双连通，又可指边双连通。（但这并不意味着它们等价）
•在图G的所有子图G’中，如果G’是双连通的，则称G’为双连通子图。如果一个双连通子图G’，它不是任何一个双连通子图的真子集（如果集合A是集合B的子集，并且集合B中至少有一个元素不属于A，那么集合A叫做集合B的真子集），则G’为极大双连通子图。双连通分量(biconnected component)，或重连通分量，就是图的极大双连通子图。特殊的，点双连通分量又叫做块。
二、Tarjan算法
•与有向图求强连通分量的Tarjan算法类似，只需通过求DFN与LOW值来得出割点与桥。
•根据定义，则有：
•如果(u,v)为树枝边，u为v的父结点，则Low(u)=Min(Low(u),Low(v))
•如果(u,v)为后向边，v不为u的父结点，则Low(u)=Min(Low(u),DFN(v))
判断割点:
•一个顶点u是割点，当且仅当满足(1)或(2)：
•(1) u为树根，且u有多于一个子树。因为如果只有一颗子树，去掉根节点后肯定不会出现多个子树，因此不可能为割点；而无向图DFS搜索树中不存在横叉边，所以若有多个子树，这些子树间不会有边相连，因此u肯定是割点。
•(2) u不为树根，且满足存在(u,v)为树枝边（即u为v在搜索树中的父亲），并使得DFN(u)<=Low(v).（因为删去u后v以及v的子树不能到达u的祖先）
判断桥:
•一条无向边(u,v)是桥，当且仅当(u,v)为树枝边，且满足DFN(u)<Low(v).（因为v想要到达u的父亲必须经过(u,v)这条边，所以删去这条边，图不连通）
•实现时，因为有重边的问题，所以需要将一条无向边拆为两条编号一样的有向边，用邻接表进行存储。在判断(u,v)是否为后向边时要注意是树枝边的反向边还是新的一条边。
三、求双连通分量
•对于点双连通分量，实际上在求割点的过程中就能顺便求出每个点双连通分量。建立一个栈，存储当前双连通分量，在搜索图时，每找到一条树枝边或后向边（非横叉边），就把这条边加入栈中。如果遇到某时满足DFN(u)<=Low(v)，说明u是一个割点，同时把边从栈顶一个个取出，直到遇到了边(u,v)为止。取出的这些边与其相连的点，组成一个点双连通分量。割点可以属于多个点双连通分量，其余点和每条边只属于且属于一个点双连通分量。（对于两个点双连通分量，最多只有一个公共点即割点）
•对于边双连通分量，求法更为简单。只需在求出所有的桥以后，把桥边删除，原图变成了多个连通块，则每个连通块就是一个边双连通分量。桥不属于任何一个边双连通分量，其余的边和每个顶点都属于且只属于一个边双连通分量。可以用并查集实现。