前缀和 对于一维数组，前缀和是一个数组的某项下标之前(包括此项元素)的所有数组元素的和。
比如定义一个数组a的前缀和数组b, 则b[i]=a[1]+a[2]+…+a[i]。
二维前缀和与一维前缀和类似，设b[i][j]表示所有b[i‘][j‘]的和(1≤i’≤i, 1≤j’≤j)。有一点像“矩形的面积”那样，把一整块区域的值都加起来。
前缀和的作用 利用前缀和求区间和。如：
问：从第L个数到第R个数的和是多少？
答：sum[L,R] = b[R] – b[L-1]
比如：sum[3,5] = b[5]-b[2]=33-5=28
二维前缀和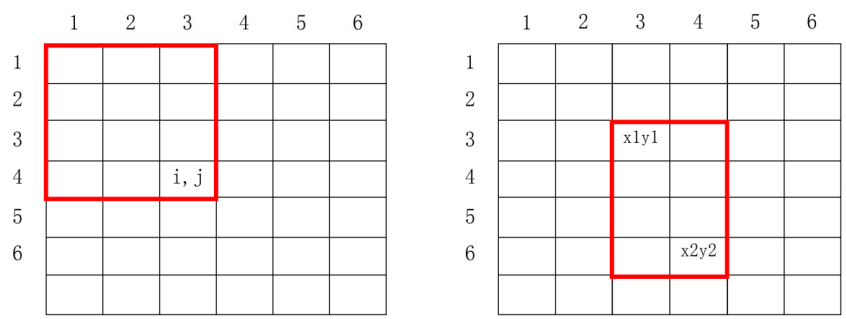
（1）s[i,j]即为图1红框中所有数的的和(前缀和)为：
s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j]
（2）根据前缀和求图2红框中的区间和为：
s[x1y1~x2y2]=s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1 ][y1-1]