什么是分层图:当同一个点可以有不同的操作时,我们将一个点分开,对应不同的操作,再重新与其他点相连。我们对每个点都进行如此操作后,原本只有一层的图就被我们分层了。
我们把样例分层,如图:
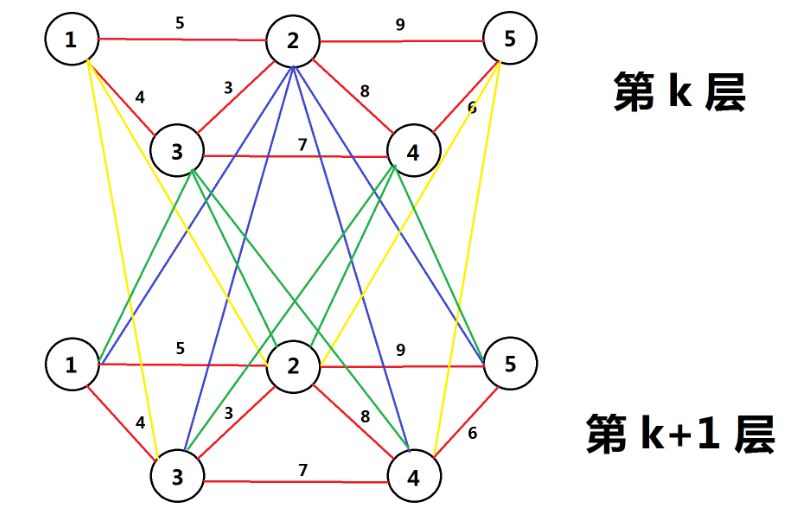
红边是普通边,其他颜色的边是进行免费操作的边。
分层图的作用:经过分层后,我们得到了新图
我们可以发现,原本题目中选 k 条边免费的操作被我们等价了:
在从一个点到另一个点时,如果选择免费,就进入下一层,相当于进行一次免费操作。
因为可以免费 k 次,所以我们要建 k+1 层图。在 k+1 层图上我们已经不能再往下了,即免费操作已用完。
那么,如何建边呢?代码实现:
for(int i=1,x,y,z;i<=p;i++){
scanf("%d%d%d",&x,&y,&z);
add(x,y,z);
add(y,x,z); //本层建边
for(int j=1,z1=0;j<=k;j++){
add(x+(j-1)*n,y+j*n,z1);//第j层和第j+1层间的建边
add(y+(j-1)*n,x+j*n,z1);
add(x+j*n,y+j*n,z);
add(y+j*n,x+j*n,z);//第j+1层建边
}
}那么,本题已经很明显可以用分层图做
但是
由于最终花费是权值最大的边
所以,在更新最短路的操作中,需要略微变动
以前我们是这么更新的:
if ( dis[y] > dis[x] + z ) dis[y] = dis[x] + z;
现在我们要这么更新:
z=max(edge,dis[x]); //edge是当前边权值
if ( dis[y] > z ) dis[y] = z;
