顺序查找（Sequential Search）又叫线性查找（Linear Search），是最基本的查找技术，它的查找过程为：从表中的第一个（或者最后一个）记录开始，逐个进行记录的关键字和给定值的比较，若某个记录的关键字和给定值比较相等，则查找成功。如果查找了所有的记录仍然找不到与给定值相等的关键字，则查找不成功。线性查找的时间复杂度为O(n)。
二分查找也叫二分搜索 (binary search)，也叫折半查找 (half-interval search)，是一种在有序数组中查找特定元素的搜索算法。所以用二分查找的前提是数组必须是有序的。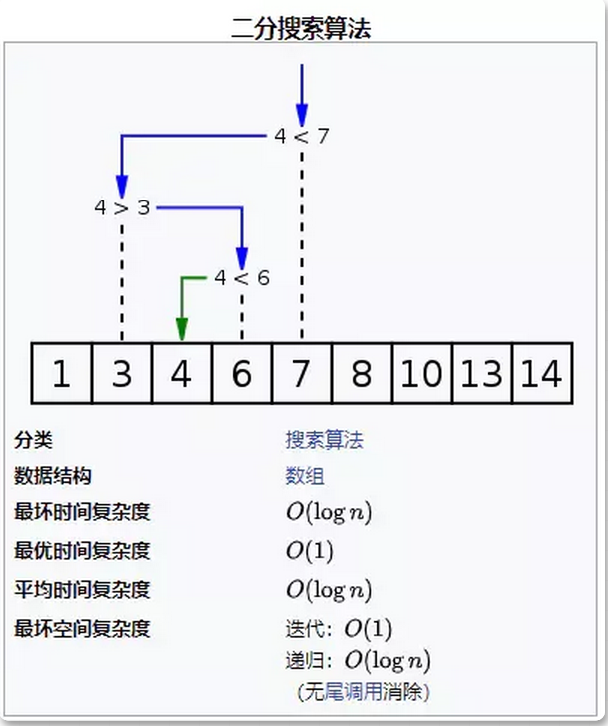
推导： 因为二分查找每次排除掉一半的不适合值，所以对于n个元素的情况：
一次二分剩下：n/2
两次二分剩下：n/2/2 = n/4
m次二分剩下：n/(2m)
在最坏情况下是在排除到只剩下最后一个值之后得到结果，即
n/(2m)=1
所以由上式可得：2m=n
进而可求出m，即时间复杂度为：log2n
如：log21, 000,000≈19.9
log2100, 000, 000≈26.6
二分法的思想是不断将待求解区间平均分成两份，根据求解区间中点的情况来确定目标元素所在的区间，这样就把解的范围缩小了一半。
二分査找常见问题
(1) 二分查找元素x在数列中是否存在(求出现位置)
(2) 二分査找左边界：第一次出现的位置( >=该元素的第1个数的位置)
(3) 二分査找右边界：第一次出现的位置( >该元素的第1个数的位置)
二分查找函数
binary_search(a+begin, a+end, x, cmp);
二分查找 函数含义：在a数组的下标为[begin, end)区间内，按照cmp的排序规则，找元素x； 找到返回true,找不到返回false。
注意点：
(1)查找区间是左闭右开的：[begin, end)，不包含结束位置；
(2)排序规则cmp不是必须的，但查找时的排序规则，必须和排序的规则是一致的；
(3)等于的含义：a等于b等价于a在b的前面，b在a的前面都不成立。
T* lower_bound(a+begin, a+end, x, cmp);
二分査找左边界 函数含义：在a数组的下标为[begin, end)区间内，按照cmp的排序规则，找元素x的 左边界(第一个 >= 元素的x的位置)，返回位置指针；
注意点：
(1)基本注意点同binary_search；
(2)此处返回的不是下标的值，而是返回指针：T* p；
(3)如果找不到符合条件的元素位置，指向下标为end的元素位置；
T* upper_bound(a+begin, a+end, x, cmp);
二分查找右边界 函数含义：在a数组的下标为[begin, end)区间内，按照cmp的排序规则，找元素x的 右边界(第一个 > 元素的x的位置)，返回位置指针；
注意点：同 lower_bound；
二分答案
最小值最大（或是最大值最小）问题常常使用二分法求解，也就是确定答案后，配合枚举、贪心等其它算法来检验这个答案是否合法，将最优化问题转变为判定性问题。
二分答案与二分査找类似，也就是对有着单调性的答案进行二分，用于求解满足某种条件下的最大(小)值。
//整数二分答案模板
while(L<=R){
int mid=(L+R)>>l;//注意L+R的数据范围，不要溢出
if(check(mid)){
ans=mid;//满足要求，记下当前最优答案，缩小范围
R=mid-l;
}else L=mid+l;
}显然，若求解的问题的定义域为整数，对于长度为N的求解区间，算法需要log2N次来确定出分界点。
//小数二分答案模板
const double EPS=1e-6; //根据题意定义允许的误差常数
double mid=(L+R)/2;
while(check(mid)>EPS){
if(check(mid)>0){
R=mid;
}else L=mid;
mid=(L+R)/2;
}注意：对于定义在实数域上的问题，因为实数运算带来的精度问题，若EPS取太小可能会导致程序死循环。
二分答案的时间复杂度为O(二分次数*单次判定复杂度)。